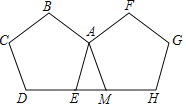
【题目】如图，两个完全相同的正五边形ABCDE，AFGHM的边DE，MH在同一直线上，且有一个公共顶点A，若正五边形ABCDE绕点A旋转x度与正五边形AFGHM重合，则x的最小值为_____．
【答案】144°.
【解析】
根据多边形的内角和定理分别求出∠BAE＝∠AED＝∠FAM＝∠AMH，即可求出∠EAM和∠BAF的度数，根据旋转的性质，分顺时针和逆时针讨论，取x的最小值.
∵五边形ABCDE，AFGHM是正五边形
∴∠BAE＝∠AED＝∠FAM＝∠AMH
108°，
∴∠AEM＝∠AME＝72°，
∴∠EAM＝180°﹣72°﹣72°＝36°，
∠BAF=360°-∠BAE -∠FAM-∠EAM=108°，
∵正五边形ABCDE绕点A旋转x度与正五边形AFGHM重合，
顺时针旋转最小需：36°+108°=144°，逆时针旋转最小需：108°+108°=216°，
∴x的最小值为36°+108°＝144°
故答案为：144°.
科目：初中数学 来源： 题型：
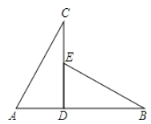
【题目】如图，已知CD⊥AB于D，现有四个条件：①AD=ED ②∠A=∠BED ③∠C=∠B ④AC=EB，那么不能得出△ADC≌△EDB的条件是（ ）.
A.①③B.②④
C.①④D.②③
查看答案和解析>>
科目：初中数学 来源： 题型：
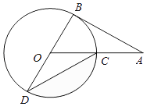
【题目】如图，AB为⊙O的切线，切点为B，连接AO，OA与⊙O交于点C，BD为⊙O的直径，连接CD，若∠A=30°，⊙O的半径为4，则图中阴影部分的面积为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场设定了一个可以自由转动的转盘（转盘被等分成16个扇形），并规定：顾客在商场消费每满200元，就能获得一次转动转盘的机会．如果转盘停止后，指针正好对准红、黄和蓝色区域，顾客就可以分别获得50元、30元和10元的购物券．如果顾客不愿意转转盘，则可以直接获得购物券15元．
(1)转动一次转盘，获得50元、30元、10元购物券的概率分别是多少？
(2)如果有一名顾客在商场消费了200元，通过计算说明转转盘和直接获得购物券，哪种方式对这位顾客更合算？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两工程队合作完成一项工程，需要12天完成，工程费用共36000元，若甲、乙两工程队单独完成此项工程，乙工程队所用的时间是甲工程队的1.5倍，乙工程队每天的费用比甲工程队少800元.
（1）问甲、乙两工程队单独完成此项工程各需多少天？
（2）若让一个工程队单独完成这项工程，哪个工程队的费用较少？
查看答案和解析>>
科目：初中数学 来源： 题型：
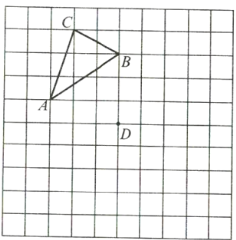
【题目】在图中网格上按要求画出图形，并回答问题：
（1）如果将三角形
平移，使得点
平移到图中点
位置，点
、点
的对应点分别为点
、点
，请画出三角形
；
（2）画出三角形关于点成中心对称的三角形
．
（3）三角形与三角形______（填“是”或“否”）关于某个点成中心对称？如果是，请在图中画出这个对称中心，并记作点
．
查看答案和解析>>
科目：初中数学 来源： 题型：
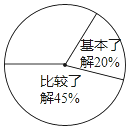
【题目】某校开展了主题为“梅山文化知多少”的专题调查活动，采取随机抽样的方式进行问卷调查，问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级，整理调查数据制成了不完整的表格和扇形统计图（如图）．
等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
频数 | 50 | m | 40 | 20 |
根据以上提供的信息解答下列问题：
（1）本次问卷调查共抽取的学生数为多少人，表中m的值为多少；
（2）计算等级为“非常了解”的频数在扇形统计图中对应扇形的圆心角的度数，并补全扇形统计图；
（3）若该校有学生2000人，请根据调查结果估计这些学生中“不太了解”梅山文化知识的人数约为多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
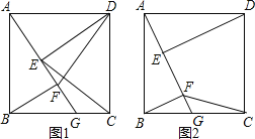
【题目】如图，四边形ABCD是正方形，点G是BC边上任意一点，DE⊥AG于点E，
且交AG于点F．
（1）求证：AE=BF；
（2）如图1，连接DF、CE，探究线段DF与CE的关系并证明；
（3）如图2，若AB=
，G为CB中点，连接CF，直接写出四边形CDEF的面积为______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在⊙O中，F，G是直径AB上的两点，C，D，E是半圆上的三点，如果弧AC的度数为60°，弧BE的度数为20°，∠CFA=∠DFB，∠DGA=∠EGB．求∠FDG的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com