
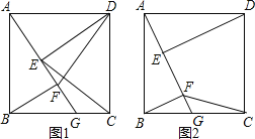
【题目】如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于点E,![]() 且交AG于点F.
且交AG于点F.
(1)求证:AE=BF;
(2)如图1,连接DF、CE,探究线段DF与CE的关系并证明;
(3)如图2,若AB=![]() ,G为CB中点,连接CF,直接写出四边形CDEF的面积为______.
,G为CB中点,连接CF,直接写出四边形CDEF的面积为______.
【答案】(1)证明见解析;(2)DF=CE且DF⊥CE,证明见解析;(3)3.
【解析】
(1)根据AAS证明![]() 即得;
即得;
(2)先根据![]() 得出
得出![]() ,再根据同角的余角相等得出
,再根据同角的余角相等得出![]() ,然后根据SAS证明
,然后根据SAS证明![]() 即得DF与CE的数量关系及
即得DF与CE的数量关系及![]() ,最后根据
,最后根据![]() 推出
推出![]() 即得DF与CE的位置关系;
即得DF与CE的位置关系;
(3)连接CE、DF,先利用勾股定理及等面积法计算出BF,在利用勾股定理及垂直平分线的性质推出DF和CE的长,最后由(2)结论可推出四边形CDEF的面积![]() 即得.
即得.
(1)证明:∵DE⊥AG于点E,BF∥DE且交AG于点F,
∴BF⊥AG于点F,∠EAD+∠ADE=90°
∴∠AED=∠BFA=90°,
∵四边形ABCD是正方形,
∴AB=AD且∠BAD=∠ADC=90°,
∴∠BAF+∠EAD=90°,
∵∠EAD+∠ADE=90°,
∴∠BAF=∠ADE,
在△AFB和△DEA中,
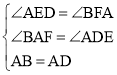 ,
,
∴△AFB≌△DEA(AAS),
∴BF=AE;
(2)DF=CE且DF⊥CE.
理由如下:∵∠FAD+∠ADE=90°,∠EDC+∠ADE=∠ADC=90°,
∴∠FAD=∠EDC,
∵△AFB≌△DEA,
∴AF=DE,
又∵四边形ABCD是正方形,
∴AD=CD,
在△FAD和△EDC中,
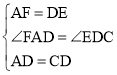
∴△FAD≌△EDC(SAS),
∴DF=CE且∠ADF=∠DCE,
∵∠ADF+∠CDF=∠ADC=90°,
∴∠DCE+∠CDF=90°,
∴DF⊥CE;
(3)如下图,连接CE、DF
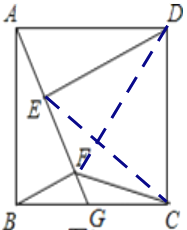
∵AB=![]() ,G为CB中点,
,G为CB中点,
∴BG=![]() BC=
BC=![]() ,
,
由勾股定理得,AG=![]() =
=![]() =
=![]() ,
,
∵S△ABG=![]() AGBF=
AGBF=![]() ABBG,
ABBG,
∴![]() ×
×![]() BF=
BF=![]() ×
×![]() ×
×![]() ,
,
解得BF=![]() ,
,
由勾股定理得,AF=![]() =
=![]() =
=![]() ,
,
∵△AFB≌△DEA,
∴AE=BF=![]() ,
,
∴AE=EF=![]() ,
,
∴DE垂直平分AF,
∴DF=AD=![]() ,
,
由(2)知,DF=CE且DF⊥CE,
∴四边形CDEF的面积=![]() DFCE=
DFCE=![]() ×
×![]() ×
×![]() =3.
=3.
故答案为:3.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
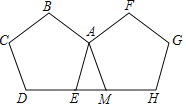
【题目】如图,两个完全相同的正五边形ABCDE,AFGHM的边DE,MH在同一直线上,且有一个公共顶点A,若正五边形ABCDE绕点A旋转x度与正五边形AFGHM重合,则x的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)我市开展了“寻找雷锋足迹”的活动,某中学为了了解七年级800名学生在“学雷锋活动月”中做好事的情况,随机调查了七年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,请根据图中提供的信息解答下列问题:
①所调查的七年级50名学生在这个月内做好事次数的平均数是 ,众数是 ,极差是 :
②根据样本数据,估计该校七年级800名学生在“学雷锋活动月”中做好事不少于4次的人数.
(2)甲口袋有2个相同的小球,它们分别写有数字1和2;乙口袋中装有3个相同的小球,它们分别写有数字3、4和5,从这两个口袋中各随机地取出1个小球.
①用“树状图法”或“列表法”表示所有可能出现的结果;
②取出的两个小球上所写数字之和是偶数的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
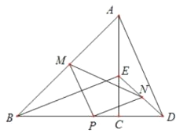
【题目】如图,已知等腰Rt△ABC和△CDE,AC=BC,CD=CE,连接BE、AD,P为BD中点,M为AB中点、N为DE中点,连接PM、PN、MN.
(1)试判断△PMN的形状,并证明你的结论;
(2)若CD=5,AC=12,求△PMN的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西安汇聚了很多人们耳熟能详的陕西美食.李华和王涛同时去选美食,李华准备在“肉夹馍(A)、羊肉泡馍(B)、麻酱凉皮(C)、(biang)面(D)”这四种美食中选择一种,王涛准备在“秘制凉皮(E)、肉丸胡辣汤(F)、葫芦鸡(G)、水晶凉皮(H)”这四种美食中选择一种.
(1)求李华选择的美食是羊肉泡馍的概率;
(2)请用画树状图或列表的方法,求李华和王涛选择的美食都是凉皮的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
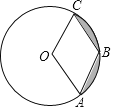
【题目】如图,已知⊙O的半径是2,点A、B、C在⊙O上,若四边形OABC为菱形,则图中阴影部分面积为( )
A. ![]() π﹣2
π﹣2![]() B.
B. ![]() π﹣
π﹣![]() C.
C. ![]() π﹣2
π﹣2![]() D.
D. ![]() π﹣
π﹣![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com