
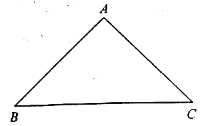
【题目】如图,![]() 中,
中,![]() ,
,![]() .
.
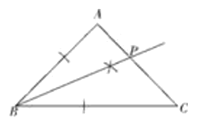
(1)请用尺规作图的方法在边![]() 上确定点
上确定点![]() ,使得
,使得![]() 平分
平分![]() ;(保留作图痕迹,不写作法)
;(保留作图痕迹,不写作法)
(2)在(1)的条件下,求证:![]() .
.
【答案】(1)图见解析;(2)详情见解析.
【解析】
(1)以B点为圆心,任意长为半径画弧交于AB与BC,然后再以交点为圆心进一步画弧找出P点即可;
(2)过P点作PD⊥BC,先利用直角三角形性质得出∠C=45°,从而进一步得出PD=CD,然后通过证明△ABP≌△DBP得出AB=BD,最后利用等量代换进一步证明即可.
(1)如图所示,P点即为所求:
(2)如图,过P点作PD⊥BC,即:∠PDC=90°,
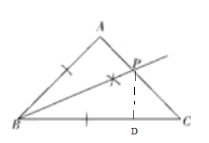
由(1)可得,BP为∠ABC的角平分线,
∴∠ABP=∠DBP,
∵![]() ,∠PDC=90°,BP为∠ABC的角平分线,
,∠PDC=90°,BP为∠ABC的角平分线,
∴PA=PD,
在![]() 中,
中,
∵![]() ,
,![]() ,
,
∴∠C=45°,
∴∠DPC=45°,
∴△PDC为等腰三角形,
∴PD=DC,
∴PD=CD=AP,
在△ABP与△DBP中,
∵∠ABP=∠DBP,![]() ∠PDC,PA=PD,
∠PDC,PA=PD,
∴△ABP≌△DBP,
∴AB=BD,
∴BD+DC=AB+AP,
即![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的切线,切点为B,连接AO,OA与⊙O交于点C,BD为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为4,则图中阴影部分的面积为( )
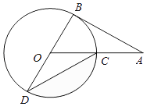
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
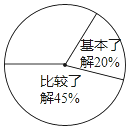
【题目】某校开展了主题为“梅山文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成了不完整的表格和扇形统计图(如图).
等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
频数 | 50 | m | 40 | 20 |
根据以上提供的信息解答下列问题:
(1)本次问卷调查共抽取的学生数为多少人,表中m的值为多少;
(2)计算等级为“非常了解”的频数在扇形统计图中对应扇形的圆心角的度数,并补全扇形统计图;
(3)若该校有学生2000人,请根据调查结果估计这些学生中“不太了解”梅山文化知识的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
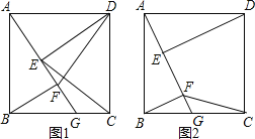
【题目】如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于点E,![]() 且交AG于点F.
且交AG于点F.
(1)求证:AE=BF;
(2)如图1,连接DF、CE,探究线段DF与CE的关系并证明;
(3)如图2,若AB=![]() ,G为CB中点,连接CF,直接写出四边形CDEF的面积为______.
,G为CB中点,连接CF,直接写出四边形CDEF的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BE平分∠ABC交AC于点E,过点E作ED∥BC交AB于点D.
(1)求证:AEBC=BDAC;
(2)如果S△ADE=3,S△BDE=2,DE=6,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
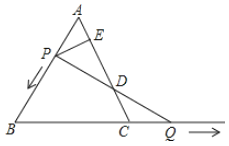
【题目】如图,![]() 是边长为3的等边三角形,
是边长为3的等边三角形,![]() 是
是![]() 边上的一个动点,由
边上的一个动点,由![]() 向
向![]() 运动(
运动(![]() 不与
不与![]() 重合),
重合),![]() 是
是![]() 延长线上一动点,与点
延长线上一动点,与点![]() 同时以相同的速度由
同时以相同的速度由![]() 向
向![]() 延长线方向运动(
延长线方向运动(![]() 不与
不与![]() 重合)
重合)
(1)当![]() 时,求
时,求![]() 的长.
的长.
(2)过![]() 作
作![]() 于点
于点![]() ,连结
,连结![]() 交
交![]() 于
于![]() ,在点
,在点![]() 的运动过程中,线段
的运动过程中,线段![]() 的长是否发生变化?若不变,求出
的长是否发生变化?若不变,求出![]() 的长度;若变化,求出变化范围.
的长度;若变化,求出变化范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,分别以AB、BC、DC为边向外作正方形,它们的面积分别为S1、S2、S3.若S2=48,S3=9,则S1的值为( )
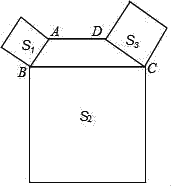
A. 18 B. 12 C. 9 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,F,G是直径AB上的两点,C,D,E是半圆上的三点,如果弧AC的度数为60°,弧BE的度数为20°,∠CFA=∠DFB,∠DGA=∠EGB.求∠FDG的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
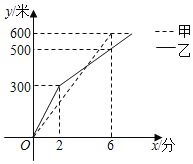
【题目】已知A、B两地相距600米,甲、乙两人同时从A地出发前往B地,所走路程y(米)与行驶时间x(分)之间的函数关系如图所示,则下列说法中:①甲每分钟走100米;②两分钟后乙每分钟走50米;③甲比乙提前3分钟到达B地;④当x=2或6时,甲乙两人相距100米.正确的有_____(在横线上填写正确的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com