
【题目】如图,![]() 是边长为3的等边三角形,
是边长为3的等边三角形,![]() 是
是![]() 边上的一个动点,由
边上的一个动点,由![]() 向
向![]() 运动(
运动(![]() 不与
不与![]() 重合),
重合),![]() 是
是![]() 延长线上一动点,与点
延长线上一动点,与点![]() 同时以相同的速度由
同时以相同的速度由![]() 向
向![]() 延长线方向运动(
延长线方向运动(![]() 不与
不与![]() 重合)
重合)
(1)当![]() 时,求
时,求![]() 的长.
的长.
(2)过![]() 作
作![]() 于点
于点![]() ,连结
,连结![]() 交
交![]() 于
于![]() ,在点
,在点![]() 的运动过程中,线段
的运动过程中,线段![]() 的长是否发生变化?若不变,求出
的长是否发生变化?若不变,求出![]() 的长度;若变化,求出变化范围.
的长度;若变化,求出变化范围.
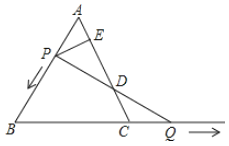
【答案】(1)1;(2)DE长度不变,且恒为1.5.
【解析】
(1)作PF∥BC交AC于F,先证明△APF为等边三角形,然后进一步得出△PFD与△QCD全等,最后进一步利用直角三角形性质求解即可;
(2)作QF⊥AC交AC的延长线于F,连接QF、PF,根据题意可知AP=CQ,进一步证明△APE与△CQF全等以及四边形PEQF为平行四边形,据此进一步求解即可.
(1)作PF∥BC交AC于F,如图1所示,
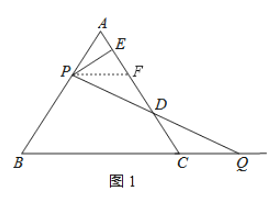
∴∠APF=∠B,∠AFP=∠ACB,∠FPD=∠CQD,∠PFD=∠QCD,
∵△ABC为等边三角形,
∴∠A=∠B=∠ACB=60°,AB=BC=AC,
∴∠APF=∠AFP=∠A=60°,
∴△APF为等边三角形,
∴AP=AF=PF,
∵Q与点P同时出发,速度也相同,
∴AP=CQ,
∴PF=CQ,
在△PFD与△QCD中,
∵∠FPD=∠CQD,PF=QC,∠PFD=∠QCD,
∴△PFD≌△QCD,
∴FD=CD,
∵![]() ,
,
∴∠APD=90°,
∵∠A=60°,
∴∠PDA=30°,
∴AD=2AP,
∴AD=2AF,
∵AF+FD=2AF
∴FD=AF,
∴AF=FD=CD,
∴AF=![]() AC,
AC,
∵AC=3,
∴AP=AF=1;
(2)DE长度不变,理由如下:
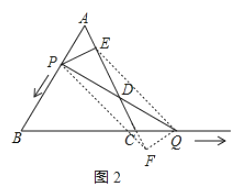
如图2所示,作QF⊥AC交AC的延长线于F,连接QF、PF,
∵![]() ,QF⊥AC,
,QF⊥AC,
∴∠DFQ=∠AEP=90°,PE∥QF,
∵点P、Q速度相同,
∴AP=CQ,
∵△ABC为等边三角形,
∴∠A=∠B=∠ACB=60°,
∴∠FCQ=60°,
∴∠A=∠FCQ,
在△APE与△CQF中,
∵∠CFQ=∠AEP=90°,
∴∠APE=∠CQF,
在△APE与△CQF中,
∵∠AEP=∠CFQ,∠A=∠FCQ,AP=CQ,
∴△APE≌△CQF,
∴AE=CF,PE=QF,
∴四边形PEQF为平行四边形,
∴DE=![]() EF,
EF,
∵AC=EC+AE=CE+CF=EF,
∴DE=![]() AC,
AC,
∵AC=3,
∴DE=1.5.
∴DE长度不变,且恒为1.5.


科目:初中数学 来源: 题型:
【题目】勾股定理有着悠久的历史,它曾引起很多人的兴趣,1955年希腊发型了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在如图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQO使得∠O=90°,点Q在在直角坐标系y轴正半轴上,点P在x轴正半轴上,点O与原点重合,∠OQP=60°,点H在边QO上,点D、E在边PO上,点G、F在边PQ上,那么点P坐标为___________.
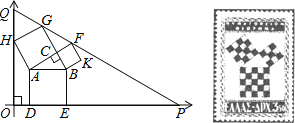
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)我市开展了“寻找雷锋足迹”的活动,某中学为了了解七年级800名学生在“学雷锋活动月”中做好事的情况,随机调查了七年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,请根据图中提供的信息解答下列问题:
①所调查的七年级50名学生在这个月内做好事次数的平均数是 ,众数是 ,极差是 :
②根据样本数据,估计该校七年级800名学生在“学雷锋活动月”中做好事不少于4次的人数.
(2)甲口袋有2个相同的小球,它们分别写有数字1和2;乙口袋中装有3个相同的小球,它们分别写有数字3、4和5,从这两个口袋中各随机地取出1个小球.
①用“树状图法”或“列表法”表示所有可能出现的结果;
②取出的两个小球上所写数字之和是偶数的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
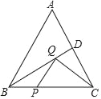
【题目】如图,等边△ABC的周长为18cm,BD为AC边上的中线,动点P,Q分别在线段BC,BD上运动,连接CQ,PQ,当BP长为_____cm时,线段CQ+PQ的和为最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西安汇聚了很多人们耳熟能详的陕西美食.李华和王涛同时去选美食,李华准备在“肉夹馍(A)、羊肉泡馍(B)、麻酱凉皮(C)、(biang)面(D)”这四种美食中选择一种,王涛准备在“秘制凉皮(E)、肉丸胡辣汤(F)、葫芦鸡(G)、水晶凉皮(H)”这四种美食中选择一种.
(1)求李华选择的美食是羊肉泡馍的概率;
(2)请用画树状图或列表的方法,求李华和王涛选择的美食都是凉皮的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
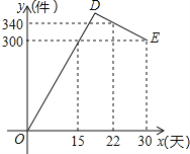
【题目】某公司开发出一款新的节能产品,该产品在正式投放市场前通过某商场,进行了为期一个月(30天)的试销售,工作人员对销售情况进行了跟踪记录,并将记录情况绘成如图所示的图象.图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系.
(1)求y与x之间的函数关系式.
(2)哪一天销售量最大?
(3)日销售量不低于320件的天数共有多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD中,点E在边DC上,DE=2,EC=1.把△ADE绕点A旋转90°,点E的对应点为点F,则F、C两点的距离为___________.
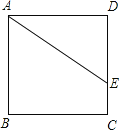
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com