
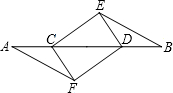
 如图,已知AF∥BE,且AF=BE,AC=BD.请指出图中有哪些全等三角形,并任选一对给予证明.
如图,已知AF∥BE,且AF=BE,AC=BD.请指出图中有哪些全等三角形,并任选一对给予证明. 分析 根据AF∥BE可得∠A=∠B,再加上条件AF=BE,AC=BD可利用SAS定理判定△ACF≌△BDE,进而可证明△ADF≌△BCE,△ECD≌△FDC.
解答 解:△ADF≌△BCE,△ECD≌△FDC,△EDB≌△FCA,
∵AF∥BE,
∴∠A=∠B,
在△ACF和△BDE中,
$\left\{\begin{array}{l}{AC=DB}\\{∠A=∠B}\\{AF=EB}\end{array}\right.$,
∴△ACF≌△BDE(SAS).
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x-y>0}\\{x+y<0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+\frac{1}{3}>\frac{1}{2}x}\\{3x≠4x-1}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{{x}^{2}+x-2>0}\\{3x<0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{3x+2y=0}\\{x>-y}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,将边长为6的正方形ABCO放置在直角坐标系中,使点A在x轴负半轴上,点C在y轴正半轴上.点M(t,0)在x轴上运动,过A作直线MC的垂线交y轴于点N.
如图,将边长为6的正方形ABCO放置在直角坐标系中,使点A在x轴负半轴上,点C在y轴正半轴上.点M(t,0)在x轴上运动,过A作直线MC的垂线交y轴于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
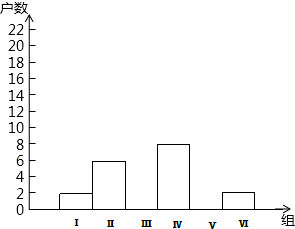 今年是我国施行“清明”小长假的第二年,在长假期间,某校团委要求学生参加一项社会调查活动.九年级学生小青想了解她所居住的小区500户居民的家庭人均收入情况,从中随机调查了40户居民家庭的人均收入情况(收入取整数,单位:元)并绘制了如下的分布表和分布图:
今年是我国施行“清明”小长假的第二年,在长假期间,某校团委要求学生参加一项社会调查活动.九年级学生小青想了解她所居住的小区500户居民的家庭人均收入情况,从中随机调查了40户居民家庭的人均收入情况(收入取整数,单位:元)并绘制了如下的分布表和分布图:| 分组 | 户数 | 百分比 |
| Ⅰ:600-799 | 2 | 0.05 |
| Ⅱ:800-999 | 6 | 0.15 |
| Ⅲ:1000-1199 | 0.45 | |
| Ⅳ:1200-1399 | 8 | 0.20 |
| Ⅴ:1400-1599 | ||
| Ⅵ:1600-1800 | 2 | 0.05 |
| 合计 | 40 | 1.00 |
| 收入情况 | 600-799 | 800-999 | 1000-1199 | 1200-1399 | 1400-1599 | 1600-1800 |
| $\frac{参加扫墓家庭数}{被调查家庭数}$ | $\frac{1}{2}$ | $\frac{1}{3}$ | $\frac{1}{6}$ | $\frac{1}{4}$ | 1 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com