
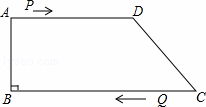
如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=12cm,BC=18cm,点P从点A出发以2cm/s的速度沿A→D→C运动,点P从点A出发的同时点Q从点C出发,以1cm/s的速度向点B运动,当点P到达点C时,点Q也停止运动.设点P,Q运动的时间为t秒.
(1)从运动开始,当t取何值时,PQ∥CD?
(2)从运动开始,当t取何值时,△PQC为直角三角形?
科目:初中数学 来源: 题型:
如题19图,已知锐角△ABC.
(1) 过点A作BC边的垂线MN,交BC于点D(用尺规作图法,保留作图痕迹,不要求写作法);
(2) 在(1)条件下,若BC=5,AD=4,tan∠BAD=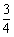 ,求DC的长.
,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:
①BE=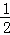 GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH
GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH
其中,正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
2014年我国的GDP总量为629180亿元,将629180亿用科学记数法表示为( )
A. 6.2918×105元 B. 6.2918×1014元
C. 6.2918×1013元 D. 6.2918×1012元
查看答案和解析>>
科目:初中数学 来源: 题型:
下列因式分解正确的是( )
A. a4b﹣6a3b+9a2b=a2b(a2﹣6a+9) B. x2﹣x+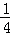 =(x﹣
=(x﹣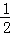 )2
)2
C. x2﹣2x+4=(x﹣2)2 D. 4x2﹣y2=(4x+y)(4x﹣y)
查看答案和解析>>
科目:初中数学 来源: 题型:
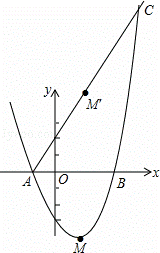
如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,顶点M关于x轴的对称点是M′.
(1)求抛物线的解析式;
(2)若直线AM′与此抛物线的另一个交点为C,求△CAB的面积;
(3)是否存在过A,B两点的抛物线,其顶点P关于x轴的对称点为Q,使得四边形APBQ为正方形?若存在,求出此抛物线的解析式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
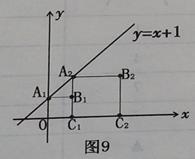
在正方形A1B1C1O和A2B2C2C1,按如图9所示方式放置,在直线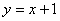
上,点C1,C2在x轴上,已知A1点的坐标是(0,1),则点B2的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com