
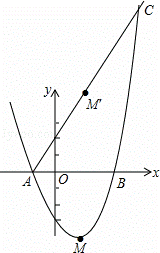
如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,顶点M关于x轴的对称点是M′.
(1)求抛物线的解析式;
(2)若直线AM′与此抛物线的另一个交点为C,求△CAB的面积;
(3)是否存在过A,B两点的抛物线,其顶点P关于x轴的对称点为Q,使得四边形APBQ为正方形?若存在,求出此抛物线的解析式;若不存在,请说明理由.
解:(1)将A、B点坐标代入函数解析式,得
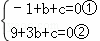 ,
,
解得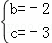 ,
,
抛物线的解析式y=x2﹣2x﹣3;
(2)将抛物线的解析式化为顶点式,得
y=(x﹣1)2﹣4,
M点的坐标为(1,﹣4),
M′点的坐标为(1,4),
设AM′的解析式为y=kx+b,
将A、M′点的坐标代入,得
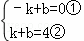 ,
,
解得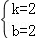 ,
,
AM′的解析式为y=2x+2,
联立AM′与抛物线,得
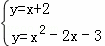 ,
,
解得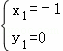 ,
,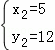
C点坐标为(5,12).
S△ABC= ×4×12=24;
×4×12=24;
(3)存在过A,B两点的抛物线,其顶点P关于x轴的对称点为Q,使得四边形APBQ为正方形,
由ABPQ是正方形,A(﹣1,0)B(3,0),得
P(1,﹣2),Q(1,2),或P(1,2),Q(1,﹣2),
①当顶点P(1,﹣2)时,设抛物线的解析式为y=a(x﹣1)2﹣2,
将A点坐标代入函数解析式,得
a(﹣1﹣1)2﹣2=0,
解得a= ,
,
抛物线的解析式为y= (x﹣1)2﹣2,
(x﹣1)2﹣2,
②当P(1,2)时,设抛物线的解析式为y=a(x﹣1)2+2,将
A点坐标代入函数解析式,得
a(﹣1﹣1)2+2=0,
解得a=﹣ ,
,
抛物线的解析式为y=﹣ (x﹣1)2+2,
(x﹣1)2+2,
综上所述:y= (x﹣1)2﹣2或y=﹣
(x﹣1)2﹣2或y=﹣ (x﹣1)2+2,使得四边形APBQ为正方形.
(x﹣1)2+2,使得四边形APBQ为正方形.


科目:初中数学 来源: 题型:
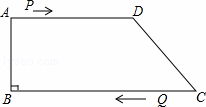
如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=12cm,BC=18cm,点P从点A出发以2cm/s的速度沿A→D→C运动,点P从点A出发的同时点Q从点C出发,以1cm/s的速度向点B运动,当点P到达点C时,点Q也停止运动.设点P,Q运动的时间为t秒.
(1)从运动开始,当t取何值时,PQ∥CD?
(2)从运动开始,当t取何值时,△PQC为直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
下列说法不正确的是( )
A.圆锥的俯视图是圆
B.对角线互相垂直平分的四边形是菱形
C.任意一个等腰三角形是钝角三角形
D.周长相 等的正方形、长方形、圆,这三个几何图形中,圆面积最大
等的正方形、长方形、圆,这三个几何图形中,圆面积最大
查看答案和解析>>
科目:初中数学 来源: 题型:
为了解某种电动汽车的性能,对这种电动汽车进行了抽检,将一次充电后行驶的里程数分为A,B,C,D四个等级,其中相应等级的里程依次为200千米,210千米,220千米,230千米,获得如下不完整的统计图。
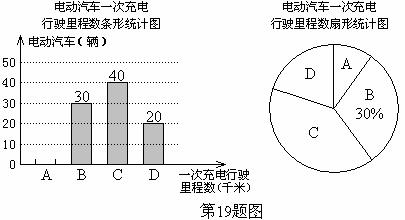
根据以上信息,解答下列问题:
(1)问这次被抽检的电动汽车共有几辆?并补全条形统计图;
(2)估计这种电动汽车一次充电后行驶的平均里程数为多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com