
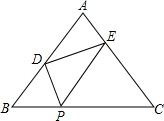
 如图,在△ABC中,AB=AC=5,BC=6,P是BC上一点,且BP=2,将一个大小与∠B相等的角的顶点放在P 点,然后将这个角绕P点转动,使角的两边始终分别与AB、AC相交,交点为D、E.
如图,在△ABC中,AB=AC=5,BC=6,P是BC上一点,且BP=2,将一个大小与∠B相等的角的顶点放在P 点,然后将这个角绕P点转动,使角的两边始终分别与AB、AC相交,交点为D、E.| 1 |
| 2 |
| BH |
| AB |
| PD |
| PE |
| 3 |
| 5 |
| BD |
| CP |
| PD |
| PE |
| 3 |
| 5 |
| 12 |
| 5 |
|
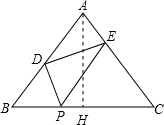 (2)作AH⊥BC于H.
(2)作AH⊥BC于H.| 1 |
| 2 |
| BH |
| AB |
| PD |
| PE |
| 3 |
| 5 |
| BD |
| CP |
| PD |
| PE |
| 3 |
| 5 |
| 12 |
| 5 |


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com