
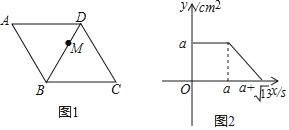
【题目】如图,已知平行四边形ABCD中,AB=BC,点M从点D出发,沿D→C→A以1cm/s的速度匀速运动到点A,图2是点M运动时,△MAB的面积y(cm2)随时间x(s)变化的关系图象,则边AB的长为( )cm.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
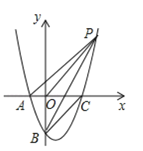
【题目】已知抛物线y=![]() x2+bx+c经过点A(﹣2,0)、B(0、﹣4)与x轴交于另一点C,连接BC.
x2+bx+c经过点A(﹣2,0)、B(0、﹣4)与x轴交于另一点C,连接BC.
(1)求抛物线的解析式.
(2)如图,P是第一象限内抛物线上一点,且![]() ,求P点坐标.
,求P点坐标.
(3)在抛物线上是否存在点D,直线BD交x轴于点E,使![]() ABE与以A,B,C,E中的三点为顶点的三角形相似(不重合)?若存在,请求出点D的坐标;若不存在,请说明理由.
ABE与以A,B,C,E中的三点为顶点的三角形相似(不重合)?若存在,请求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
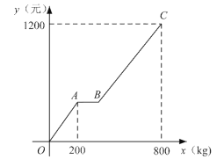
【题目】某商店代理销售一种水果,六月份的销售利润![]() (元)与销售量
(元)与销售量![]() 之间函数关系的图像如图中折线所示.请你根据图像及这种水果的相关销售记录提供的信息,解答下列问题:
之间函数关系的图像如图中折线所示.请你根据图像及这种水果的相关销售记录提供的信息,解答下列问题:
日期 | 销售记录 |
6月1日 | 库存 |
6月9日 | 从6月1日至今,一共售出 |
6月10、11日 | 这两天以成本价促销,之后售价恢复到10元/ |
6月12日 | 补充进货 |
6月30日 |
|
(1)截止到6月9日,该商店销售这种水果一共获利多少元?
(2)求图像中线段![]() 所在直线对应的函数表达式.
所在直线对应的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
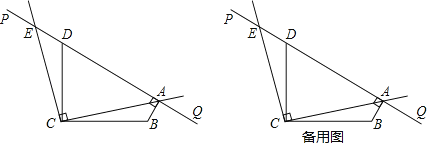
【题目】如图,∠BCD=90°,BC=DC,直线PQ经过点D.设∠PDC=α(45°<α<135°),BA⊥PQ于点A,将射线CA绕点C按逆时针方向旋转90°,与直线PQ交于点E.
(1)判断:∠ABC ∠PDC(填“>”或“=”或“<”);
(2)猜想△ACE的形状,并说明理由;
(3)若△ABC的外心在其内部(不含边界),直接写出α的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学为了深入学习社会主义核心价值观,特对本校部分学生(随机抽样)进行了一次相关知识的测试(成绩分为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、五个组,
、五个组,![]() 表示测试成绩),通过对测试成绩的分析,得到如图所示的两幅不完整的统计图,请你根据图中提供的信息解答以下问题.
表示测试成绩),通过对测试成绩的分析,得到如图所示的两幅不完整的统计图,请你根据图中提供的信息解答以下问题.
![]() 组:
组:![]()
![]() 组:
组:![]()
![]() 组:
组:![]()
![]() 组:
组:![]()
![]() 组:
组:![]()
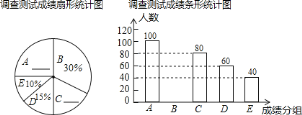
![]() 参加调查测试的学生共有________人;请将两幅统计图补充完整.
参加调查测试的学生共有________人;请将两幅统计图补充完整.
![]() 本次调查测试成绩的中位数落在________组内.
本次调查测试成绩的中位数落在________组内.
![]() 本次调查测试成绩在
本次调查测试成绩在![]() 分以上(含
分以上(含![]() 分)为优秀,该中学共有
分)为优秀,该中学共有![]() 人,请估计全校测试成绩为优秀的学生有多少人?
人,请估计全校测试成绩为优秀的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数 y=ax2+bx﹣(a+b)(a,b 是常数,a≠0).
(1)判断该二次函数图象与 x 轴的交点的个数,说明理由.
(2)若该二次函数图象经过 A(﹣1,4),B(0,﹣1),C(1,1)三个点中的其中两个点,求该二次函数的表达式.
(3)若 a+b<0,点 P(2,m)(m>0)在该二次函数图象上,求证:a>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年夏季全国各地总有未成年人因溺水而丧失生命,令人痛心疾首.今年我校为确保学生安全,开展了“远离溺水珍爱生命”的防溺水安全知识竞赛.现从七、八年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用x表示,共分成四组:A.80≤x<85,B.85≤x<90,C.90≤x<95,D.95≤x≤100),下面给出了部分信息:
七年级10名学生的竞赛成绩是:99,80,99,86,99,96,90,100,89,82 ;
八年级10名学生的竞赛成绩在C组中的数据是:92,90,94.
七、八年级抽取的学生竞赛成绩统计表

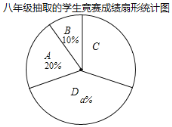
根据以上信息,解答下列问题:
(1)上述图表中a=______,b=______,c=______;
(2) 我校七、八年级共400人参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀(x≥90)的学生人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国魏晋时期著名的数学家刘徽在《九章算术》中提出了“割圆术——割之弥细,所失弥少,隔之又割,以至不可割,则与圆周合体,而无所失也.”也就是利用圆的内接多边形逐步逼近圆的方法来近似计算圆的面积和周长.如图1,若用圆的内接正六边形的面积![]() 来近似估计半径为1的⊙O的面积,再用如图2的圆的内接正十二边形的面积
来近似估计半径为1的⊙O的面积,再用如图2的圆的内接正十二边形的面积![]() 来近似估计半径为1的⊙O的面积,则
来近似估计半径为1的⊙O的面积,则![]() ____.(结果保留根号)
____.(结果保留根号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com