
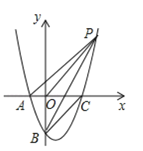
【题目】已知抛物线y=![]() x2+bx+c经过点A(﹣2,0)、B(0、﹣4)与x轴交于另一点C,连接BC.
x2+bx+c经过点A(﹣2,0)、B(0、﹣4)与x轴交于另一点C,连接BC.
(1)求抛物线的解析式.
(2)如图,P是第一象限内抛物线上一点,且![]() ,求P点坐标.
,求P点坐标.
(3)在抛物线上是否存在点D,直线BD交x轴于点E,使![]() ABE与以A,B,C,E中的三点为顶点的三角形相似(不重合)?若存在,请求出点D的坐标;若不存在,请说明理由.
ABE与以A,B,C,E中的三点为顶点的三角形相似(不重合)?若存在,请求出点D的坐标;若不存在,请说明理由.
【答案】(1)y=![]() x2﹣x﹣4;(2)P (6,8);(3)存在,D (8,20)或
x2﹣x﹣4;(2)P (6,8);(3)存在,D (8,20)或![]()
【解析】
(1)利用待定系数法求抛物线的解析式;
(2)令y=0求抛物线与x轴的交点C的坐标,作△POB和△PBC的高线,根据面积相等可得OG=CF,证明△OEG≌△CEF,得OE=CE,即得到点E的坐标为(2,0),利用待定系数法求得直线PB的解析式,解方程组即可求得P点坐标;
(3)先利用概率的知识分析A,B,C,E中的三点为顶点的三角形,有两个三角形与△ABE有可能相似,即△ABC和△BCE,
①当△ABE与以A,B,C中的三点为顶点的三角形相似,如图2,根据存在公共角∠BAE=∠BAC,可得△ABE∽△ACB,列比例式可得E的坐标,利用待定系数法求直线BE的解析式,与抛物线列方程组可得交点D的坐标;
②当△ABE与以B,C、E中的三点为顶点的三角形相似,如图3,同理可得结论.
(1)把点A(-2,0),B(0、-4)代入抛物线![]() 得:
得:
![]() ,
,
解得:![]() ,
,
∴抛物线的解析式为![]() ;
;
(2)当![]() 时,
时,![]() ,
,
解得:![]() 或4,
或4,
∴点C的坐标为(4,0),
如图1,过O作OG⊥BP于G,过C作CF⊥BP于F,PB交![]() 轴于点E,
轴于点E,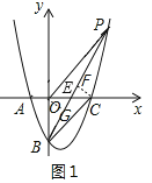
∵S△PBO=S△PBC,
∴![]() BPOG=
BPOG=![]() BPCF,
BPCF,
∴OG=CF,
∵∠OEG=∠CEF,∠OGE∠CFE,
∴△OEG≌△CEF(AAS),
∴OE=CE,
点E的坐标为(2,0),
设直线PB的解析式为![]() ,
,
把点E(2,0)代入得,![]()
解得:![]() ,
,
∴直线PB的解析式为![]() ,
,
解方程组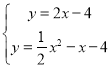 得:
得: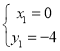 (舍去)或
(舍去)或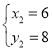 ,
,
∴点P的坐标为(6,8);
(3)以A,B,C,E中的三点为顶点的三角形有△ABC、△ABE、△ACE、△BCE,四种,其中△ABE重合,不符合条件,△ACE不能构成三角形,
∴当△ABE与以A,B,C,E中的三点为顶点的三角形相似,存在两个三角形:△ABC和△BCE,
①当△ABE与以A,B,C中的三点为顶点的三角形相似,如图2,
(3)以A,B,C,E中的三点为顶点的三角形有△ABC、△ABE、△ACE、△BCE,四种,其中△ABE重合,不符合条件,△ACE不能构成三角形,
∴当△ABE与以A,B,C,E中的三点为顶点的三角形相似,存在两个三角形:△ABC和△BCE,
①当△ABE与以A,B,C中的三点为顶点的三角形相似,如图2,
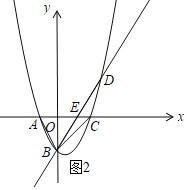
由(1)得:点A(-2,0),B(0,-4),C(4,0),
∴OB=OC=4,
![]() ,
,
![]() ,
,
∴∠OBC=∠OCB=45°,
∵∠BAE=∠BAC,∠ABE≠∠ABC,
∴∠ABE=∠ACB=45°,
∴△ABE∽△ACB,
∴![]() ,
,
∴![]() ,
,
解得:![]() ,
,![]() ,
,
点![]() 的坐标为(
的坐标为(![]() ,0);
,0);
设直线BE的解析式为![]() ,
,
把点E(![]() ,0)代入得,
,0)代入得,![]() ,
,
∴直线BE的解析式为![]() ,
,
解方程组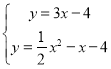 得:
得: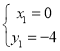 (舍去)或
(舍去)或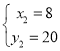 ,
,
∴点D的坐标为(8,20);
②当△ABE与以B,C、E中的三点为顶点的三角形相似,如图3,此时E在C的左边,
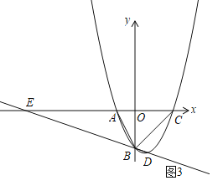
∵∠BEA=∠BEC,
∴当∠ABE=∠BCE时,△ABE∽△BCE,
∴![]() ,
,
设![]() ,
,![]() ,
,
Rt△BOE中,由勾股定理得:![]() ,
,
∴![]() ,
,
即![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 或
或![]() ,
,
∵![]() ,∠AEB或∠BEC是钝角,如图4,此时△ABE与以B,C、E中的三点为顶点的三角形不相似,
,∠AEB或∠BEC是钝角,如图4,此时△ABE与以B,C、E中的三点为顶点的三角形不相似,
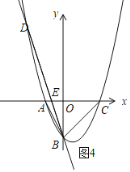
∴E(-12,0);
同理得BE的解析式为:![]() ,
,
解方程组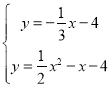 得:
得: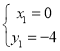 (舍去)或
(舍去)或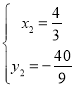 ,
,
∴点D的坐标为(![]() ,
,![]() );
);
同理可得E在C的右边时,△ABE∽△BCE,
∴![]() ,
,
设![]() ,
,![]() ,
,
Rt△BOE中,由勾股定理得:![]() ,
,
∴![]() ,
,
即![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() (舍去)或
(舍去)或![]() ,
,
∵![]() ,∠BEC是钝角,此时△ABE与以B,C、E中的三点为顶点的三角形不相似,
,∠BEC是钝角,此时△ABE与以B,C、E中的三点为顶点的三角形不相似,
综上,点D的坐标为(8,20)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过点
经过点![]() ,
,![]() .
.
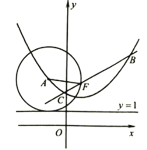
(1)求![]() 的值,并将抛物线解析式化成顶点式;
的值,并将抛物线解析式化成顶点式;
(2)已知点![]() ,点
,点![]() 为抛物线上一动点.求证:以
为抛物线上一动点.求证:以![]() 为圆心,
为圆心,![]() 为半径的圆与直线
为半径的圆与直线![]() 相切;
相切;
(3)在(2)的条件下,点![]() 为抛物线上一动点,作直线
为抛物线上一动点,作直线![]() ,与抛物线交于点
,与抛物线交于点![]() .当
.当![]() 时,请直接写出直线
时,请直接写出直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场第一次用11000元购进某款拼装机器人进行销售,很快销售一空,商家又用24000元第二次购进同款机器人,所购进数量是第一次的2倍,但单价贵了10元.
(1)求该商家第一次购进机器人多少个?
(2)若所有机器人都按相同的标价销售,要求全部销售完毕的利润率不低于20%(不考虑其它因素),那么每个机器人的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陈钢和王昊两人从甲市开车前往乙市,甲、乙两市的行使路程为180千米.已知王昊行使速度是陈钢行使速度的1.5倍,若陈钢比王昊早出发0.5小时,结果陈钢比王昊晚到0.5小时,求陈钢、王昊两人的行使速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
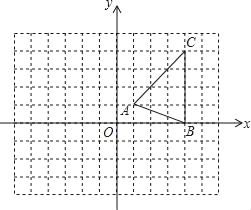
【题目】如图,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,1),B(4,0),C(4,4).
(1)按下列要求作图:
①将△ABC向左平移4个单位,得到△A1B1C1;
②将△A1B1C1绕点B1逆时针旋转90°,得到△A2B2C2.
(2)求点C1在旋转过程中所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】合理饮食对学生的身体、智力发育和健康起到了极其重要的作用,只有荤食和素食的合理搭配,才能强化初中生的身体素质,某校为了解学生的体质健康状况,以便食堂为学生提供合理膳食,对本校七年级、八年级学生的体质健康状况进行了调查,过程如下:
收集数据:
从七、八年级两个年级中各抽取![]() 名学生,进行了体质健康测试,测试成绩(百分制)如下:
名学生,进行了体质健康测试,测试成绩(百分制)如下:
七年级:![]()
八年级:![]()
整理数据:
年级 |
|
|
|
|
七年级 |
|
|
|
|
八年级 |
|
|
|
|
(说明:![]() 为优秀,
为优秀,![]() 为良好,
为良好,![]() 为及格,
为及格,![]() 为不及格)
为不及格)
分析数据:
年级 | 平均数 | 中位数 | 众数 |
七年级 |
|
|
|
八年级 |
|
|
|
(1)表格中![]() ,
,![]() ,
,![]() ,
,
(2)比较这两组样本数据的平均数、中位数和众数,你认为哪个年级的体质健康成绩比较好?请说明理由
(3)若七年级共有![]() 名学生,请估计七年级体质健康成绩优秀的学生人数
名学生,请估计七年级体质健康成绩优秀的学生人数
查看答案和解析>>
科目:初中数学 来源: 题型:
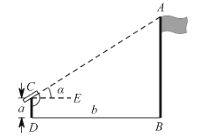
【题目】如图,小明想要测量学校操场上旗杆![]() 的高度,他作了如下操作:(1)在点
的高度,他作了如下操作:(1)在点![]() 处放置测角仪,测得旗杆顶的仰角
处放置测角仪,测得旗杆顶的仰角![]() ;(2)量得测角仪的高度
;(2)量得测角仪的高度![]() ;(3)量得测角仪到旗杆的水平距离
;(3)量得测角仪到旗杆的水平距离![]() .利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )
.利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
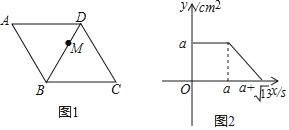
【题目】如图,已知平行四边形ABCD中,AB=BC,点M从点D出发,沿D→C→A以1cm/s的速度匀速运动到点A,图2是点M运动时,△MAB的面积y(cm2)随时间x(s)变化的关系图象,则边AB的长为( )cm.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解同学们最喜欢一年四季中的哪个季节,数学社在全校随机抽取部分同学进行问卷调查,根据调查结果,得到如下两幅不完整的统计图.

根据图中信息,解答下列问题:
(1)此次调查一共随机抽取了________名同学;扇形统计图中,“春季”所对应的扇形的圆心角的度数为________;
(2)若该学校有1500名同学,请估计该校最喜欢冬季的同学的人数;
(3)现从最喜欢夏季的3名同学A,B,C中,随机选两名同学去参加学校组织的“我爱夏天”演讲比赛,请用列表或画树状图的方法求恰好选到A,B去参加比赛的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com