
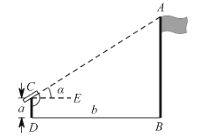
【题目】如图,小明想要测量学校操场上旗杆![]() 的高度,他作了如下操作:(1)在点
的高度,他作了如下操作:(1)在点![]() 处放置测角仪,测得旗杆顶的仰角
处放置测角仪,测得旗杆顶的仰角![]() ;(2)量得测角仪的高度
;(2)量得测角仪的高度![]() ;(3)量得测角仪到旗杆的水平距离
;(3)量得测角仪到旗杆的水平距离![]() .利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )
.利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
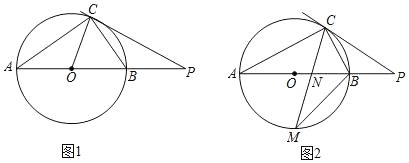
【题目】已知,AB是⊙O的直径,点C在⊙O上,点P是AB延长线上一点,连接CP.
(1)如图1,若∠PCB=∠A.
①求证:直线PC是⊙O的切线;
②若CP=CA,OA=2,求CP的长;
(2)如图2,若点M是弧AB的中点,CM交AB于点N,MNMC=9,求BM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
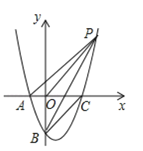
【题目】已知抛物线y=![]() x2+bx+c经过点A(﹣2,0)、B(0、﹣4)与x轴交于另一点C,连接BC.
x2+bx+c经过点A(﹣2,0)、B(0、﹣4)与x轴交于另一点C,连接BC.
(1)求抛物线的解析式.
(2)如图,P是第一象限内抛物线上一点,且![]() ,求P点坐标.
,求P点坐标.
(3)在抛物线上是否存在点D,直线BD交x轴于点E,使![]() ABE与以A,B,C,E中的三点为顶点的三角形相似(不重合)?若存在,请求出点D的坐标;若不存在,请说明理由.
ABE与以A,B,C,E中的三点为顶点的三角形相似(不重合)?若存在,请求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
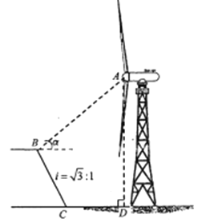
【题目】风能作为一种清洁能源越来越受到世界各国的重视,我省多地结合自身地理优势架设风力发电机利用风能发电.王芳和李华假期去大理巍山游玩,看见风电场的各个山头上布满了大大小小的风力发电机,好奇的想知道风力发电机塔架的高度.如图,王芳站在坡度![]() ,坡面长
,坡面长![]() 的斜坡
的斜坡![]() 的底部
的底部![]() 点测得
点测得![]() 点与塔底
点与塔底![]() 点的距离为
点的距离为![]() ,此时,李华在坡顶
,此时,李华在坡顶![]() 点测得轮毂
点测得轮毂![]() 点的仰角
点的仰角![]() ,请根据测量结果帮他们计算风力发电机塔架
,请根据测量结果帮他们计算风力发电机塔架![]() 的高度.(结果精确到
的高度.(结果精确到![]() ,参考数据
,参考数据![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
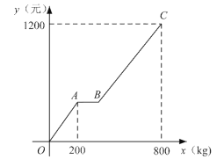
【题目】某商店代理销售一种水果,六月份的销售利润![]() (元)与销售量
(元)与销售量![]() 之间函数关系的图像如图中折线所示.请你根据图像及这种水果的相关销售记录提供的信息,解答下列问题:
之间函数关系的图像如图中折线所示.请你根据图像及这种水果的相关销售记录提供的信息,解答下列问题:
日期 | 销售记录 |
6月1日 | 库存 |
6月9日 | 从6月1日至今,一共售出 |
6月10、11日 | 这两天以成本价促销,之后售价恢复到10元/ |
6月12日 | 补充进货 |
6月30日 |
|
(1)截止到6月9日,该商店销售这种水果一共获利多少元?
(2)求图像中线段![]() 所在直线对应的函数表达式.
所在直线对应的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
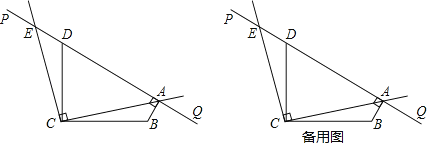
【题目】如图,∠BCD=90°,BC=DC,直线PQ经过点D.设∠PDC=α(45°<α<135°),BA⊥PQ于点A,将射线CA绕点C按逆时针方向旋转90°,与直线PQ交于点E.
(1)判断:∠ABC ∠PDC(填“>”或“=”或“<”);
(2)猜想△ACE的形状,并说明理由;
(3)若△ABC的外心在其内部(不含边界),直接写出α的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数 y=ax2+bx﹣(a+b)(a,b 是常数,a≠0).
(1)判断该二次函数图象与 x 轴的交点的个数,说明理由.
(2)若该二次函数图象经过 A(﹣1,4),B(0,﹣1),C(1,1)三个点中的其中两个点,求该二次函数的表达式.
(3)若 a+b<0,点 P(2,m)(m>0)在该二次函数图象上,求证:a>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将函数![]() 为常数)的图象记为
为常数)的图象记为![]() 图象
图象![]() 与直线
与直线![]() 的交点坐标为
的交点坐标为![]() .
.
(1)若点![]() 在图象
在图象![]() 上,求
上,求![]() 的值;
的值;
(2)求![]() 的最小值;
的最小值;
(3)当直线![]() 的图象与函数
的图象与函数![]() 为常数)的图像只有一个公共点时,求
为常数)的图像只有一个公共点时,求![]() 的取值范围;
的取值范围;
(4)若![]() 点
点![]() 在图象
在图象![]() 上,且点
上,且点![]() 的横坐标为
的横坐标为![]() 点
点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() .当点
.当点![]() 不在坐标轴上时,以点
不在坐标轴上时,以点![]() 为顶点构造矩形
为顶点构造矩形![]() 使点
使点![]() 落在
落在![]() 轴上.当图象
轴上.当图象![]() 与矩形
与矩形![]() 的边有两个公共点时,直接写出
的边有两个公共点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com