
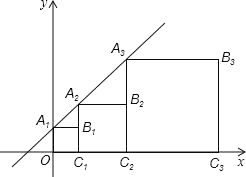
【题目】正方形![]() 、
、![]() 、
、![]() 、…按如图所示的方式放置,点
、…按如图所示的方式放置,点![]() 、
、![]() 、
、![]() 、…和点
、…和点![]() 、
、![]() 、
、![]() 、…分别在直线
、…分别在直线![]() 和
和![]() 轴上,则点
轴上,则点![]() 的坐标是__________.(答案不需要化简)
的坐标是__________.(答案不需要化简)
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过点
经过点![]() ,
,![]() .
.
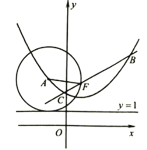
(1)求![]() 的值,并将抛物线解析式化成顶点式;
的值,并将抛物线解析式化成顶点式;
(2)已知点![]() ,点
,点![]() 为抛物线上一动点.求证:以
为抛物线上一动点.求证:以![]() 为圆心,
为圆心,![]() 为半径的圆与直线
为半径的圆与直线![]() 相切;
相切;
(3)在(2)的条件下,点![]() 为抛物线上一动点,作直线
为抛物线上一动点,作直线![]() ,与抛物线交于点
,与抛物线交于点![]() .当
.当![]() 时,请直接写出直线
时,请直接写出直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段铁路的示意图,![]() 段和
段和![]() 段都是高架桥,
段都是高架桥,![]() 段是隧道.已知
段是隧道.已知![]() ,
,![]() ,
,![]() ,在
,在![]() 段高架桥上有一盏吊灯,当火车驶过时,灯光可垂直照射到车身上,已知火车甲沿
段高架桥上有一盏吊灯,当火车驶过时,灯光可垂直照射到车身上,已知火车甲沿![]() 方向匀速行驶,当火车甲经过吊灯时,灯光照射到火车甲上的时间是
方向匀速行驶,当火车甲经过吊灯时,灯光照射到火车甲上的时间是![]() ,火车甲通过隧道的时间是
,火车甲通过隧道的时间是![]() ,如果从车尾经过点
,如果从车尾经过点![]() 时开始计时,设行驶的时间为
时开始计时,设行驶的时间为![]() ,车头与点
,车头与点![]() 的距离是
的距离是![]() .
.

(1)火车甲的速度和火车甲的长度
(2)求![]() 关于
关于![]() 的函数解析式(写出
的函数解析式(写出![]() 的取值范围),并求当
的取值范围),并求当![]() 为何值时,车头差
为何值时,车头差![]() 米到达
米到达![]() 点.
点.
(3)若长度相等的火车乙以相同的速度沿![]() 方向行驶,且火车甲乙不在隧道内会车(会车时两车均不在隧道内),火车甲先进隧道,当火车甲的车头到达
方向行驶,且火车甲乙不在隧道内会车(会车时两车均不在隧道内),火车甲先进隧道,当火车甲的车头到达![]() 点时,火车乙的车头能否到达
点时,火车乙的车头能否到达![]() 点?若能到达,至多驶过地点多少?若不能到达,至少距离
点?若能到达,至多驶过地点多少?若不能到达,至少距离![]() 点多少
点多少![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形 ABCD 中,AB=5,AD=13,点 E 为 BC 上一点,将△ABE沿 AE 折叠,使点 B 落在长方形内点 F 处,连接 DF 且 DF=12.

(1)试说明:△ADF 是直角三角形;
(2)求 BE 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
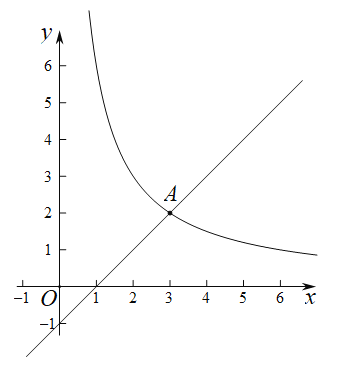
【题目】在平面直角坐标系![]() 中,反比例函数
中,反比例函数![]() 的图象与直线
的图象与直线![]() 交于点
交于点![]()
(1)求k的值;
(2)已知点![]() ,过点P作垂直于x轴的直线,交直线
,过点P作垂直于x轴的直线,交直线![]() 于点B,交函数
于点B,交函数![]() 于点C.
于点C.
①当![]() 时,判断线段
时,判断线段![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
②若![]() ,结合图象,直接写出n的取值范围.
,结合图象,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场第一次用11000元购进某款拼装机器人进行销售,很快销售一空,商家又用24000元第二次购进同款机器人,所购进数量是第一次的2倍,但单价贵了10元.
(1)求该商家第一次购进机器人多少个?
(2)若所有机器人都按相同的标价销售,要求全部销售完毕的利润率不低于20%(不考虑其它因素),那么每个机器人的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
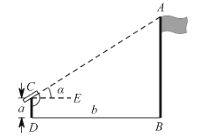
【题目】如图,小明想要测量学校操场上旗杆![]() 的高度,他作了如下操作:(1)在点
的高度,他作了如下操作:(1)在点![]() 处放置测角仪,测得旗杆顶的仰角
处放置测角仪,测得旗杆顶的仰角![]() ;(2)量得测角仪的高度
;(2)量得测角仪的高度![]() ;(3)量得测角仪到旗杆的水平距离
;(3)量得测角仪到旗杆的水平距离![]() .利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )
.利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com