
ĄūĖâÄŋĄŋČįÍžĢŽŌŧķÎĖú·ĩÄĘūŌâÍžĢŽ![]() ķΚÍ
ķΚÍ![]() ķÎķžĘĮļßžÜĮÅĢŽ
ķÎķžĘĮļßžÜĮÅĢŽ![]() ķÎĘĮËíĩĀĢŪŌŅÖŠ
ķÎĘĮËíĩĀĢŪŌŅÖŠ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŽÔÚ
ĢŽÔÚ![]() ķÎļßžÜĮÅÉÏÓÐŌŧÕĩĩõĩÆĢŽĩąŧðģĩĘŧđýĘąĢŽĩÆđâŋÉīđÖąÕÕÉäĩ―ģĩÉíÉÏĢŽŌŅÖŠŧðģĩžŨŅØ
ķÎļßžÜĮÅÉÏÓÐŌŧÕĩĩõĩÆĢŽĩąŧðģĩĘŧđýĘąĢŽĩÆđâŋÉīđÖąÕÕÉäĩ―ģĩÉíÉÏĢŽŌŅÖŠŧðģĩžŨŅØ![]() ·―ÏōÔČËŲÐÐĘŧĢŽĩąŧðģĩžŨūđýĩõĩÆĘąĢŽĩÆđâÕÕÉäĩ―ŧðģĩžŨÉÏĩÄĘąžäĘĮ
·―ÏōÔČËŲÐÐĘŧĢŽĩąŧðģĩžŨūđýĩõĩÆĘąĢŽĩÆđâÕÕÉäĩ―ŧðģĩžŨÉÏĩÄĘąžäĘĮ![]() ĢŽŧðģĩžŨÍĻđýËíĩĀĩÄĘąžäĘĮ
ĢŽŧðģĩžŨÍĻđýËíĩĀĩÄĘąžäĘĮ![]() ĢŽČįđûīÓģĩÎēūđýĩã
ĢŽČįđûīÓģĩÎēūđýĩã![]() ĘąŋŠĘžžÆĘąĢŽÉčÐÐĘŧĩÄĘąžäΊ
ĘąŋŠĘžžÆĘąĢŽÉčÐÐĘŧĩÄĘąžäΊ![]() ĢŽģĩÍ·Óëĩã
ĢŽģĩÍ·Óëĩã![]() ĩÄūāĀëĘĮ
ĩÄūāĀëĘĮ![]() ĢŪ
ĢŪ

ĢĻ1ĢĐŧðģĩžŨĩÄËŲķČšÍŧðģĩžŨĩÄģĪķČ
ĢĻ2ĢĐĮó![]() đØÓÚ
đØÓÚ![]() ĩÄšŊĘý―âÎöĘ―ĢĻÐīģö
ĩÄšŊĘý―âÎöĘ―ĢĻÐīģö![]() ĩÄČĄÖĩ·ķΧĢĐĢŽēĒĮóĩą
ĩÄČĄÖĩ·ķΧĢĐĢŽēĒĮóĩą![]() ΊšÎÖĩĘąĢŽģĩÍ·ēî
ΊšÎÖĩĘąĢŽģĩÍ·ēî![]() ÃŨĩ―īï
ÃŨĩ―īï![]() ĩãĢŪ
ĩãĢŪ
ĢĻ3ĢĐČôģĪķČÏāĩČĩÄŧðģĩŌŌŌÔÏāÍŽĩÄËŲķČŅØ![]() ·―ÏōÐÐĘŧĢŽĮŌŧðģĩžŨŌŌēŧÔÚËíĩĀÄÚŧáģĩĢĻŧáģĩĘąÁ―ģĩūųēŧÔÚËíĩĀÄÚĢĐĢŽŧðģĩžŨÏČ―øËíĩĀĢŽĩąŧðģĩžŨĩÄģĩÍ·ĩ―īï
·―ÏōÐÐĘŧĢŽĮŌŧðģĩžŨŌŌēŧÔÚËíĩĀÄÚŧáģĩĢĻŧáģĩĘąÁ―ģĩūųēŧÔÚËíĩĀÄÚĢĐĢŽŧðģĩžŨÏČ―øËíĩĀĢŽĩąŧðģĩžŨĩÄģĩÍ·ĩ―īï![]() ĩãĘąĢŽŧðģĩŌŌĩÄģĩÍ·ÄÜ·ņĩ―īï
ĩãĘąĢŽŧðģĩŌŌĩÄģĩÍ·ÄÜ·ņĩ―īï![]() ĩãĢŋČôÄÜĩ―īïĢŽÖÁķāĘŧđýĩØĩãķāÉŲĢŋČôēŧÄÜĩ―īïĢŽÖÁÉŲūāĀë
ĩãĢŋČôÄÜĩ―īïĢŽÖÁķāĘŧđýĩØĩãķāÉŲĢŋČôēŧÄÜĩ―īïĢŽÖÁÉŲūāĀë![]() ĩãķāÉŲ
ĩãķāÉŲ![]() Ģŋ
Ģŋ
Ąūīð°ļĄŋĢĻ1ĢĐŧðģĩžŨĩÄËŲķČĘĮ![]() ĢŽŧðģĩžŨĩÄģĪĘĮ
ĢŽŧðģĩžŨĩÄģĪĘĮ![]() ĢŧĢĻ2ĢĐ
ĢŧĢĻ2ĢĐ![]() ĢŽ
ĢŽ![]() ĢŧĢĻ3ĢĐŧðģĩŌŌģĩÍ·ēŧÄÜĩ―īï
ĢŧĢĻ3ĢĐŧðģĩŌŌģĩÍ·ēŧÄÜĩ―īï![]() ĩãĢŽÖÁÉŲūāĀë
ĩãĢŽÖÁÉŲūāĀë![]() ĩã
ĩã![]()
Ąū―âÎöĄŋ
ĢĻ1ĢĐÉčŧðģĩžŨĩÄËŲķČĘĮ![]() ĢŽŧðģĩžŨĩÄģĪĘĮ
ĢŽŧðģĩžŨĩÄģĪĘĮ![]() ĢŽÓÉĖâŌâÁÐģö·―ģĖŨéĢŽ―â·―ģĖŨéžīŋÉĢŧ
ĢŽÓÉĖâŌâÁÐģö·―ģĖŨéĢŽ―â·―ģĖŨéžīŋÉĢŧ
ĢĻ2ĢĐÓÉĖâŌâĢŽŋÉ·ÖΊĢšĩąģĩÍ·ĩ―īï![]() ĩãĮ°ĢŧĩąģĩÍ·ÔÚ
ĩãĮ°ĢŧĩąģĩÍ·ÔÚ![]() ĩãĘąĢŧĩąģĩÍ·ūđý
ĩãĘąĢŧĩąģĩÍ·ūđý![]() ĩãšóĢŧ·ÖąðĮóģö―âÎöĘ―ĢŽžīŋÉĩÃĩ―īð°ļĢŧ
ĩãšóĢŧ·ÖąðĮóģö―âÎöĘ―ĢŽžīŋÉĩÃĩ―īð°ļĢŧ
ĢĻ3ĢĐļųūÝĖâŌâĢŽÕŌģöĩČÁŋđØÏĩĢŽÁÐģöĩČĘ――øÐÐ―âĖâžīŋÉĢŪ
―âĢšĢĻ1ĢĐÉčŧðģĩžŨĩÄËŲķČĘĮ![]() ĢŽŧðģĩžŨĩÄģĪĘĮ
ĢŽŧðģĩžŨĩÄģĪĘĮ![]()
ÓÉĖâŌâĩÃ![]()
―âĩÃ![]()
īðĢšŧðģĩžŨĩÄËŲķČĘĮ![]() ĢŽŧðģĩžŨĩÄģĪĘĮ
ĢŽŧðģĩžŨĩÄģĪĘĮ![]()
ĢĻ2ĢĐĩąģĩÍ·ĩ―īï![]() ĩãĮ°ĢŽžī
ĩãĮ°ĢŽžī![]() ĘąĢŽ
ĘąĢŽ
![]()
ĩąģĩÍ·ÔÚ![]() ĩãĘąĢŽ
ĩãĘąĢŽ![]() Ģŧ
Ģŧ
ĩąģĩÍ·ūđý![]() ĩãšóĢŽžī
ĩãšóĢŽžī![]() Ęą
Ęą
![]()
ŨÛÉÏ![]()
ĩąģĩÍ·ēî![]() ÃŨÎīĩ―īï
ÃŨÎīĩ―īï![]() ĩãĘąĢŽ
ĩãĘąĢŽ![]() ĢŽ
ĢŽ
žī![]()
―âĩÃ![]()
Ąāĩą![]() ĘąĢŽģĩÍ·ēî
ĘąĢŽģĩÍ·ēî![]() ÃŨÎīĩ―īï
ÃŨÎīĩ―īï![]() ĩãĢŧ
ĩãĢŧ
ĢĻ3ĢĐŧðģĩžŨīÓģĩÍ·ĩ―īï![]() ĩãĢŽĩ―ģĩÎēĀëŋŠËíĩĀĢŽđēÓÃĘą
ĩãĢŽĩ―ģĩÎēĀëŋŠËíĩĀĢŽđēÓÃĘą![]() ĢŽ
ĢŽ
ŌōīËŌŠĘđÁ―ÁÐŧðģĩēŧÔÚËíĩĀÄÚŧáģĩĢŽÔōĩąŧðģĩžŨģĩÍ·ĩ―īï![]() ĩãĘąĢŽŧðģĩŌŌĩÄģĩÍ·ūā
ĩãĘąĢŽŧðģĩŌŌĩÄģĩÍ·ūā![]() ĩãÖÁÉŲŌŠÓÐ
ĩãÖÁÉŲŌŠÓÐ![]() ĩÄģĩģĖĢŽŌēūÍĘĮ
ĩÄģĩģĖĢŽŌēūÍĘĮ![]() ĢŽ
ĢŽ
Ąß![]()
ĄāĩąŧðģĩžŨģĩÍ·ĩ―īï![]() ĩãĘąĢŽŧðģĩŌŌģĩÍ·ēŧÄÜĩ―īï
ĩãĘąĢŽŧðģĩŌŌģĩÍ·ēŧÄÜĩ―īï![]() ĩãĢŽÖÁÉŲūāĀë
ĩãĢŽÖÁÉŲūāĀë![]() ĩã
ĩã![]() Ģŧ
Ģŧ


 ŋÎĖÃČŦ―âŨÖīĘūäķÎÆŠÕÂÏĩÁÐīð°ļ
ŋÎĖÃČŦ―âŨÖīĘūäķÎÆŠÕÂÏĩÁÐīð°ļ ē―ē―ļßŋÚËãĖâŋĻÏĩÁÐīð°ļ
ē―ē―ļßŋÚËãĖâŋĻÏĩÁÐīð°ļ ĩãūĶÐÂ―ĖēÄČŦÄÜ―âķÁÏĩÁÐīð°ļ
ĩãūĶÐÂ―ĖēÄČŦÄÜ―âķÁÏĩÁÐīð°ļ
| Äęžķ | ļßÖÐŋÎģĖ | Äęžķ | ģõÖÐŋÎģĖ |
| ļßŌŧ | ļßŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõŌŧ | ģõŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßķþ | ļßķþÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõķþ | ģõķþÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßČý | ļßČýÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõČý | ģõČýÃâ·ŅŋÎģĖÍÆžöĢĄ |
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋđÅÏĢĀ°ÖøÃûĩÄąÏīïļįĀËđŅ§ÅÉ°Ņ1ĄĒ3ĄĒ6ĄĒ10ĄĒĄĄÕâŅųĩÄĘýģÆΊĄ°Čý―ĮÐÎĘýĄąĢŽķø°Ņ1ĄĒ4ĄĒ16ĄĒĄĄÕâŅųĩÄĘýģÆΊĄ°Õý·―ÐÎĘýĄąĢŪīÓÍžÖÐŋÉŌÔ·ĒÏÖĢŽČΚÎŌŧļöīóÓÚ1ĩÄĄ°Õý·―ÐÎĘýĄąķžŋÉŌÔŋīŨũÁ―ļöÏāÁÚĄ°Čý―ĮÐÎĘýĄąÖŪšÍĢŪ°īÏÂÁÐÍžĘūÖÐĩÄđæÂÉĢŽĮëÐīģöĩÚ9ļöĩČĘ―_____ĢŪ

ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽÔÚÖą―ĮŨøąęÏĩÖÐĢŽÖąÏßy=Đ![]() xÓë·īąČĀýšŊĘýy=
xÓë·īąČĀýšŊĘýy=![]() ĩÄÍžÏó―ŧÓÚđØÓÚÔĩãķÔģÆĩÄAĢŽBÁ―ĩãĢŽŌŅÖŠAĩãĩÄŨÝŨøąęĘĮ3ĢŪ
ĩÄÍžÏó―ŧÓÚđØÓÚÔĩãķÔģÆĩÄAĢŽBÁ―ĩãĢŽŌŅÖŠAĩãĩÄŨÝŨøąęĘĮ3ĢŪ
ĢĻ1ĢĐĮó·īąČĀýšŊĘýĩÄąíīïĘ―Ģŧ
ĢĻ2ĢĐ―ŦÖąÏßy=Đ![]() xÏōÉÏÆ―ŌÆšóÓë·īąČĀýšŊĘýÔÚĩÚķþÏóÏÞÄÚ―ŧÓÚĩãCĢŽČįđûĄũABCĩÄÃæŧýΊ48ĢŽĮóÆ―ŌÆšóĩÄÖąÏßĩÄšŊĘýąíīïĘ―ĢŪ
xÏōÉÏÆ―ŌÆšóÓë·īąČĀýšŊĘýÔÚĩÚķþÏóÏÞÄÚ―ŧÓÚĩãCĢŽČįđûĄũABCĩÄÃæŧýΊ48ĢŽĮóÆ―ŌÆšóĩÄÖąÏßĩÄšŊĘýąíīïĘ―ĢŪ

ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČôŌŧīΚŊĘý![]() ĩÄÍžÏóÓë
ĩÄÍžÏóÓë![]() ÖáĢŽ
ÖáĢŽ![]() Öá·Öąð―ŧÓÚAĢŽCÁ―ĩãĢŽĩãBĩÄŨøąęΊ
Öá·Öąð―ŧÓÚAĢŽCÁ―ĩãĢŽĩãBĩÄŨøąęΊ![]() ĢŽķþīΚŊĘý
ĢŽķþīΚŊĘý![]() ĩÄÍžÏóđýAĢŽBĢŽCČýĩãĢŽČįÍžĢĻ1ĢĐĢŪ
ĩÄÍžÏóđýAĢŽBĢŽCČýĩãĢŽČįÍžĢĻ1ĢĐĢŪ
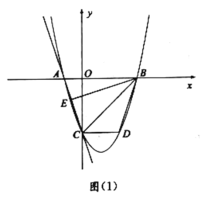
ĢĻ1ĢĐĮóķþīΚŊĘýĩÄąíīïĘ―Ģŧ
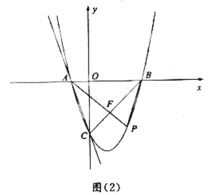
ĢĻ2ĢĐČįÍžĢĻ1ĢĐĢŽđýĩãCŨũ![]() Öá―ŧÅŨÎïÏßÓÚĩãDĢŽĩãEÔÚÅŨÎïÏßÉÏĢĻ
Öá―ŧÅŨÎïÏßÓÚĩãDĢŽĩãEÔÚÅŨÎïÏßÉÏĢĻ![]() ÖáŨóēāĢĐĢŽČô
ÖáŨóēāĢĐĢŽČô![]() ĮĄšÃÆ―·Ö
ĮĄšÃÆ―·Ö![]() ĢŪĮóÖąÏß
ĢŪĮóÖąÏß![]() ĩÄąíīïĘ―Ģŧ
ĩÄąíīïĘ―Ģŧ
ĢĻ3ĢĐČįÍžĢĻ2ĢĐĢŽČôĩãPÔÚÅŨÎïÏßÉÏĢĻĩãPÔÚ![]() ÖáÓŌēāĢĐĢŽÁŽ―Ó
ÖáÓŌēāĢĐĢŽÁŽ―Ó![]() ―ŧ
―ŧ![]() ÓÚĩãFĢŽÁŽ―Ó
ÓÚĩãFĢŽÁŽ―Ó![]() ĢŽ
ĢŽ![]() ĢŪ
ĢŪ
ĒŲĩą![]() ĘąĢŽĮóĩãPĩÄŨøąęĢŧ
ĘąĢŽĮóĩãPĩÄŨøąęĢŧ
ĒÚĮó![]() ĩÄŨîīóÖĩĢŪ
ĩÄŨîīóÖĩĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽÁâÐÎ![]() ÖÐĢŽķÔ―ĮÏß
ÖÐĢŽķÔ―ĮÏß![]() ĄĒ
ĄĒ![]() Ïā―ŧÓÚĩã
Ïā―ŧÓÚĩã![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŽķŊĩã
ĢŽķŊĩã![]() īÓĩã
īÓĩã![]() ģö·ĒĢŽŅØÏßķÎ
ģö·ĒĢŽŅØÏßķÎ![]() ŌÔ
ŌÔ![]() ĩÄËŲķČÏōĩã
ĩÄËŲķČÏōĩã![]() ÔËķŊĢŽÍŽĘąķŊĩã
ÔËķŊĢŽÍŽĘąķŊĩã![]() īÓĩã
īÓĩã![]() ģö·ĒĢŽŅØÏßķÎ
ģö·ĒĢŽŅØÏßķÎ![]() ŌÔ
ŌÔ![]() Ö§Ïōĩã
Ö§Ïōĩã![]() ÔËķŊĢŽĩąÆäÖÐŌŧļöķŊĩãÍĢÖđĘąÁíŌŧļöķŊĩãŌēËæÖŪÍĢÖđĢŽÉčÔËķŊĘąžäΊ
ÔËķŊĢŽĩąÆäÖÐŌŧļöķŊĩãÍĢÖđĘąÁíŌŧļöķŊĩãŌēËæÖŪÍĢÖđĢŽÉčÔËķŊĘąžäΊ![]() ĢĻĩĨÎŧĢš
ĢĻĩĨÎŧĢš![]() ĢĐĢĻ
ĢĐĢĻ![]() ĢĐĢŽŌÔĩã
ĢĐĢŽŌÔĩã![]() ΊÔēÐÄĢŽ
ΊÔēÐÄĢŽ![]() ģĪΊ°ëūķĩÄĄŅMÓëÉäÏß
ģĪΊ°ëūķĩÄĄŅMÓëÉäÏß![]() ĄĒÏßķÎ
ĄĒÏßķÎ![]() ·Öąð―ŧÓÚĩã
·Öąð―ŧÓÚĩã![]() ĄĒ
ĄĒ![]() ĢŽÁŽ―Ó
ĢŽÁŽ―Ó![]() ĢŪ
ĢŪ
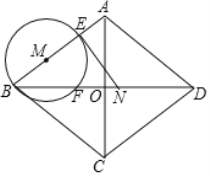
ĢĻ1ĢĐĮó![]() ĩÄģĪĢĻÓÚŽÓÐ
ĩÄģĪĢĻÓÚŽÓÐ![]() ĩÄīúĘýĘ―ąíĘūĢĐĢŽēĒĮóģö
ĩÄīúĘýĘ―ąíĘūĢĐĢŽēĒĮóģö![]() ĩÄČĄÖĩ·ķΧĢŧ
ĩÄČĄÖĩ·ķΧĢŧ
ĢĻ2ĢĐĩą![]() ΊšÎÖĩĘąĢŽÏßķÎ
ΊšÎÖĩĘąĢŽÏßķÎ![]() ÓëĄŅMÏāĮÐĢŋ
ÓëĄŅMÏāĮÐĢŋ
ĢĻ3ĢĐČôĄŅMÓëÏßķÎ![]() ÖŧÓÐŌŧļöđŦđēĩãĢŽĮó
ÖŧÓÐŌŧļöđŦđēĩãĢŽĮó![]() ĩÄČĄÖĩ·ķΧĢŪ
ĩÄČĄÖĩ·ķΧĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
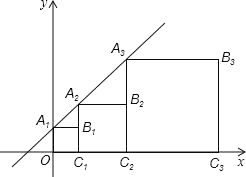
ĄūĖâÄŋĄŋÕý·―ÐÎ![]() ĄĒ
ĄĒ![]() ĄĒ
ĄĒ![]() ĄĒĄ°īČįÍžËųĘūĩÄ·―Ę―·ÅÖÃĢŽĩã
ĄĒĄ°īČįÍžËųĘūĩÄ·―Ę―·ÅÖÃĢŽĩã![]() ĄĒ
ĄĒ![]() ĄĒ
ĄĒ![]() ĄĒĄšÍĩã
ĄĒĄšÍĩã![]() ĄĒ
ĄĒ![]() ĄĒ
ĄĒ![]() ĄĒĄ·ÖąðÔÚÖąÏß
ĄĒĄ·ÖąðÔÚÖąÏß![]() šÍ
šÍ![]() ÖáÉÏĢŽÔōĩã
ÖáÉÏĢŽÔōĩã![]() ĩÄŨøąęĘĮ__________ĢŪĢĻīð°ļēŧÐčŌŠŧŊžōĢĐ
ĩÄŨøąęĘĮ__________ĢŪĢĻīð°ļēŧÐčŌŠŧŊžōĢĐ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍž1ĢŽÅŨÎïÏßyĢ―ax2Đ6ax+6ĢĻaĄŲ0ĢĐÓëxÖá―ŧÓÚĩãAĢĻ8ĢŽ0ĢĐĢŽÓëyÖá―ŧÓÚĩãBĢŽÔÚxÖáÉÏÓÐŌŧķŊĩãEĢĻmĢŽ0ĢĐĢĻ0ĢžmĢž8ĢĐĢŽđýĩãEŨũxÖáĩÄīđÏß―ŧÖąÏßABÓÚĩãNĢŽ―ŧÅŨÎïÏßÓÚĩãPĢŽđýĩãPŨũPMĄÍABÓÚĩãMĢŪ
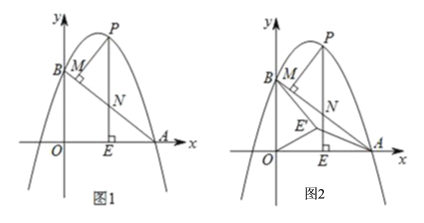
ĢĻ1ĢĐĮóģöÅŨÎïÏßĩÄšŊĘýąíīïĘ―Ģŧ
ĢĻ2ĢĐÉčĄũPMNĩÄÃæŧýΊS1ĢŽĄũAENĩÄÃæŧýΊS2ĢŽČôS1ĢšS2Ģ―36Ģš25ĢŽĮómĩÄÖĩĢŧ
ĢĻ3ĢĐČįÍž2ĢŽÔÚĢĻ2ĢĐĖõžþÏÂĢŽ―ŦÏßķÎOEČÆĩãOÄæĘąÕëÐýŨŠĩÃĩ―OEĄäĢŽÐýŨŠ―ĮΊ30ĄãĢŽÁŽ―ÓE'AĄĒE'BĢŽÔÚŨøąęÆ―ÃæÄÚÕŌŌŧĩãQĢŽĘđĄũAOEĄäĄŦĄũBOQĢŽēĒĮóģöQĩÄŨøąęĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽÅŨÎïÏßyĢ―Ģx2ĢŦbxĢŦcÓëxÖáÏā―ŧÓÚAĢĻĢ1ĢŽ0ĢĐĢŽBĢĻ5ĢŽ0ĢĐÁ―ĩãĢŪ
ĢĻ1ĢĐĮóÅŨÎïÏßĩÄ―âÎöĘ―Ģŧ
ĢĻ2ĢĐÔÚĩÚķþÏóÏÞÄÚČĄŌŧĩãCĢŽŨũCDīđÖąxÖáÓÚĩãDĢŽÁī―ÓACĢŽĮŌADĢ―5ĢŽCDĢ―8ĢŽ―ŦRtĄũACDŅØxÖáÏōÓŌÆ―ŌÆmļöĩĨÎŧĢŽĩąĩãCÂäÔÚÅŨÎïÏßÉÏĘąĢŽĮómĩÄÖĩĢŧ
ĢĻ3ĢĐÔÚĢĻ2ĢĐĩÄĖõžþÏÂĢŽĩąĩãCĩÚŌŧīÎÂäÔÚÅŨÎïÏßÉÏžĮΊĩãEĢŽĩãPĘĮÅŨÎïÏßķÔģÆÖáÉÏŌŧĩãĢŪĘÔĖ―ūŋĢšÔÚÅŨÎïÏßÉÏĘĮ·ņīæÔÚĩãQĢŽĘđŌÔĩãBĄĒEĄĒPĄĒQΊķĨĩãĩÄËÄąßÐÎĘĮÆ―ÐÐËÄąßÐÎĢŋČôīæÔÚĢŽĮëģöĩãQĩÄŨøąęĢŧČôēŧīæÔÚĢŽĮëËĩÃũĀíÓÉĢŪ

ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
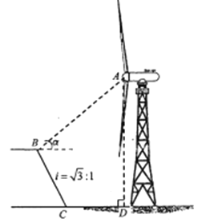
ĄūĖâÄŋĄŋ·įÄÜŨũΊŌŧÖÖĮå―āÄÜÔīÔ―ĀīÔ―ĘÜĩ―ĘĀ―įļũđúĩÄÖØĘÓĢŽÎŌĘĄķāĩØ―ášÏŨÔÉíĩØĀíÓÅĘÆžÜÉč·įÁĶ·ĒĩįŧúĀûÓ÷įÄÜ·Ēĩį.Íõ·žšÍĀîŧŠžŲÆÚČĨīóĀíÎĄÉ―ÓÎÍæĢŽŋīžû·įĩįģĄĩÄļũļöÉ―Í·ÉÏēžÂúÁËīóīóÐĄÐĄĩÄ·įÁĶ·ĒĩįŧúĢŽšÃÆæĩÄÏëÖŠĩĀ·įÁĶ·ĒĩįŧúËþžÜĩÄļßķČ.ČįÍžĢŽÍõ·žÕūÔÚÆÂķČ![]() ĢŽÆÂÃæģĪ
ĢŽÆÂÃæģĪ![]() ĩÄÐąÆÂ
ĩÄÐąÆÂ![]() ĩÄĩŨēŋ
ĩÄĩŨēŋ![]() ĩãēâĩÃ
ĩãēâĩÃ![]() ĩãÓëËþĩŨ
ĩãÓëËþĩŨ![]() ĩãĩÄūāĀëΊ
ĩãĩÄūāĀëΊ![]() ĢŽīËĘąĢŽĀîŧŠÔÚÆÂķĨ
ĢŽīËĘąĢŽĀîŧŠÔÚÆÂķĨ![]() ĩãēâĩÃÂÖėą
ĩãēâĩÃÂÖėą![]() ĩãĩÄŅö―Į
ĩãĩÄŅö―Į![]() ĢŽĮëļųūÝēâÁŋ―áđû°ïËûÃĮžÆËã·įÁĶ·ĒĩįŧúËþžÜ
ĢŽĮëļųūÝēâÁŋ―áđû°ïËûÃĮžÆËã·įÁĶ·ĒĩįŧúËþžÜ![]() ĩÄļßķČĢŪĢĻ―áđûūŦČ·ĩ―
ĩÄļßķČĢŪĢĻ―áđûūŦČ·ĩ―![]() ĢŽēÎŋžĘýūÝ
ĢŽēÎŋžĘýūÝ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢĐ
ĢĐ
ēéŋīīð°ļšÍ―âÎö>>
đúžĘŅ§ÐĢÓÅŅĄ - Á·Ï°ēáÁÐąí - ĘÔĖâÁÐąí
šþąąĘĄŧĨÁŠÍøÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻÆ―ĖĻ | ÍøÉÏÓКĶÐÅÏĒūŲąĻŨĻĮø | ĩįÐÅÕĐÆūŲąĻŨĻĮø | ÉæĀúĘ·ÐéÎÞÖũŌåÓКĶÐÅÏĒūŲąĻŨĻĮø | ÉæÆóĮÖČĻūŲąĻŨĻĮø
ÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻĩįŧ°Ģš027-86699610 ūŲąĻÓĘÏäĢš58377363@163.com