
����Ŀ����ͼ������![]() �У��Խ���
�У��Խ���![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��![]() ��
��![]() ������
������![]() �ӵ�
�ӵ�![]() ���������߶�
���������߶�![]() ��
��![]() ���ٶ����
���ٶ����![]() �˶���ͬʱ����
�˶���ͬʱ����![]() �ӵ�
�ӵ�![]() ���������߶�
���������߶�![]() ��
��![]() ֧���
֧���![]() �˶���������һ������ֹͣʱ��һ������Ҳ��ֹ֮ͣ�����˶�ʱ��Ϊ
�˶���������һ������ֹͣʱ��һ������Ҳ��ֹ֮ͣ�����˶�ʱ��Ϊ![]() ����λ��
�����![]() ����
����![]() �����Ե�
�����Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() ��Ϊ�뾶�ġ�M������
��Ϊ�뾶�ġ�M������![]() ���߶�
���߶�![]() �ֱ��ڵ�
�ֱ��ڵ�![]() ��
��![]() ������
������![]() ��
��
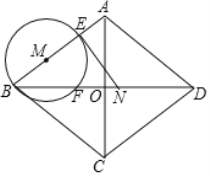
��1����![]() �ij����ú���
�ij����ú���![]() �Ĵ���ʽ��ʾ���������
�Ĵ���ʽ��ʾ���������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����![]() Ϊ��ֵʱ���߶�
Ϊ��ֵʱ���߶�![]() ���M���У�
���M����
��3������M���߶�![]() ֻ��һ�������㣬��
ֻ��һ�������㣬��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���𰸡�������BF=![]() t��0��t��8����������t=
t��0��t��8����������t=![]() ��������0��t��
��������0��t��![]() ��
��![]() ��t��8
��t��8
��������
��1������MB=MF��AB=AD���Ƴ�MF��AD����ƽ���߷��߶γɱ����ɵ�![]() �������BF�ij���
�������BF�ij���
��2�����߶�EN���M����ʱ����֪��BEN�ס�BOA���ٸ��ݶ�Ӧ�߳ɱ�����⼴�ɣ�
��3�����ݻ�ͼ��֪����0��t��![]() ʱ����M���߶�ENֻ��һ�������㣬��F��N�غϺ��M���߶�ENֻ��һ�������㣬���F��N�غ�ʱt��ֵ���ɣ�
ʱ����M���߶�ENֻ��һ�������㣬��F��N�غϺ��M���߶�ENֻ��һ�������㣬���F��N�غ�ʱt��ֵ���ɣ�
��1������MF����ͼ��
![]()
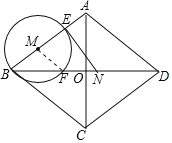
���ı���ABCD�����Σ�
��AB=AD��AC��BD��OA=OC=6��OB=OD=8��
��Rt��AOB��![]() ��
��
��MB=MF��AB=AD��
���ABD=��ADB=��MFB��
��MF��AD��
��![]() ,
,
��![]() ,
,
��BF=![]() t��0��t��8��.
t��0��t��8��.
��2�����߶�EN���M����ʱ����֪��BEN�ס�BOA��
��![]() ��
��
��![]() ��
��
��t=![]() ��
��
��t=![]() sʱ���߶�EN���M����.
sʱ���߶�EN���M����.
��3���ٸ����������֪������0��t��![]() ʱ����M���߶�ENֻ��һ��������.
ʱ����M���߶�ENֻ��һ��������.
�ڵ�F��N�غ�ʱ������![]() t+2t=16������ó�t=
t+2t=16������ó�t=![]() ��
��
����ͼ�����֪����![]() ��t��8ʱ����M���߶�ENֻ��һ��������.
��t��8ʱ����M���߶�ENֻ��һ��������.
������������0��t��![]() ��
��![]() ��t��8ʱ����M���߶�ENֻ��һ�������㣮
��t��8ʱ����M���߶�ENֻ��һ�������㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
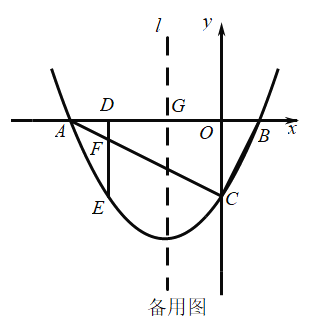
����Ŀ����֪������y=![]() ��ͼ����
��ͼ����![]() ���һ������ΪA��-1��0������һ������ΪB����
���һ������ΪA��-1��0������һ������ΪB����![]() �ύ�ڵ�C��0����3��������ΪD��
�ύ�ڵ�C��0����3��������ΪD��
��1������κ����Ľ���ʽ�͵�D�����ꣻ
��2������M����������![]() ���·�ͼ���ϵ�һ���㣬����M��MN��
���·�ͼ���ϵ�һ���㣬����M��MN��![]() �ύ�߶�BC�ڵ�N����MNȡ���ֵʱ����M �����ꣻ
�ύ�߶�BC�ڵ�N����MNȡ���ֵʱ����M �����ꣻ
��3���������������ϻ�����ƽ�ƣ�ʹ���������ߵĶ���D����x���ϣ�ԭ��������һ��Pƽ�ƺ�Ķ�Ӧ��ΪQ�������OQP=��OPQ�������Q�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
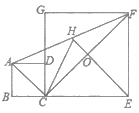
����Ŀ����ͼ��������![]() ��������
��������![]() ����
����![]() ��
��![]() �ϣ�
�ϣ�![]() ��
��![]() ��
��![]() ��
��![]() ���е㣬
���е㣬![]() ��
��![]() ���ڵ�0����
���ڵ�0����![]() �ij�Ϊ__________��
�ij�Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
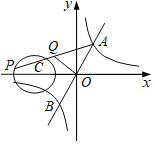
����Ŀ����ͼ��һ�κ���y=2x�뷴��������y=![]() ��k��0����ͼ����A��B���㣬��P����C����2��0��ΪԲ�ģ�1Ϊ�뾶�ġ�C�ϣ�Q��AP���е㣬��֪OQ�������ֵΪ
��k��0����ͼ����A��B���㣬��P����C����2��0��ΪԲ�ģ�1Ϊ�뾶�ġ�C�ϣ�Q��AP���е㣬��֪OQ�������ֵΪ![]() ����k��ֵΪ��������
����k��ֵΪ��������
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��
��![]() �Ḻ���ύ�ڵ�
�Ḻ���ύ�ڵ�![]() ����
����![]() �������ύ�ڵ�
�������ύ�ڵ�![]() ����
����![]() �Ḻ���ύ�ڵ�
�Ḻ���ύ�ڵ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��1�����![]() ������������ߵĺ�����ϵʽ��
������������ߵĺ�����ϵʽ��
��2����![]() ��
��![]() ��һ�㣨�����
��һ�㣨�����![]() ��
��![]() �غϣ�������
�غϣ�������![]() ��
��![]() ��Ĵ��ߣ����������ڵ�
��Ĵ��ߣ����������ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ����
����![]() ʱ�����
ʱ�����![]() �����ꣻ
�����ꣻ
��3���������ߵĶԳ���![]() ��
��![]() ���ڵ�
���ڵ�![]() ���ڣ�2���������£���
���ڣ�2���������£���![]() �������߶Գ�����һ�㣬��
�������߶Գ�����һ�㣬��![]() ������ƽ����һ�㣬�Ƿ���ڵ�
������ƽ����һ�㣬�Ƿ���ڵ�![]() ��
��![]() ��ʹ��
��ʹ��![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı��������Σ������ڣ��������
Ϊ������ı��������Σ������ڣ��������![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
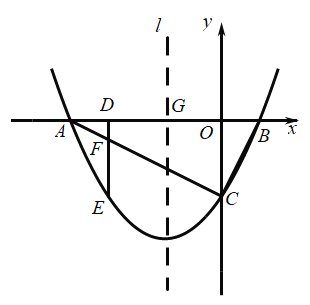
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���ѧ���������ʣ�ijУ������չ�������������������������������Ҫ��ȫԱ���룬����ÿ��ѧ��ֻ��ѡ������һ��.Ϊ�˽�ѡ������������Ŀ��ѧ����������У�����ȡ�˲���ѧ�����е��飬�����Ƴ�����������������ͳ��ͼ�������ͳ��ͼ�ش��������⣺
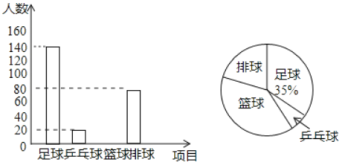
��1��ֱ��д����γ��������ѧ��������
��2����ȫ����ͳ��ͼ��
��3������ѧУ��������1500�ˣ������ѡ��������Ŀ��ѧ��Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() �У�
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() �ֱ��DZ�
�ֱ��DZ�![]() ��
��![]() �ϵĶ��㣬��
�ϵĶ��㣬��![]() ����
����![]() ����
����![]() �ĶԳƵ�
�ĶԳƵ�![]() ǡ������
ǡ������![]() ���ڽ�ƽ�����ϣ���
���ڽ�ƽ�����ϣ���![]() ��Ϊ_______________��
��Ϊ_______________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������IJ�����װ��![]() ������
������![]() ����������ɸ��������dz���ɫ�������ͬ��������������
����������ɸ��������dz���ɫ�������ͬ��������������![]() �����ǰ���ĸ���Ϊ
�����ǰ���ĸ���Ϊ![]() ��
��
��1�����������ĸ���_______��
��2��С����С���������еİ���ȡ��![]() ��������ʣ�µ������������Ϸ������Լ����������
��������ʣ�µ������������Ϸ������Լ����������![]() ����Żأ�������
����Żأ�������![]() ���������������к�����С��ʤ������С��ʤ������Ϊ�����Ϸ��ƽ�������б�����״ͼ˵�����ɣ�
���������������к�����С��ʤ������С��ʤ������Ϊ�����Ϸ��ƽ�������б�����״ͼ˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��CD����E��ֱ��AB�ϵĵ㣬����E��ֱ��l��ֱ��CD�ڵ�F��EGƽ�֡�BEF��CD�ڵ�G����ֱ��l�Ƶ�E��ת�Ĺ����У�ͼ�С�1����2�Ķ������Էֱ��ǣ� ��
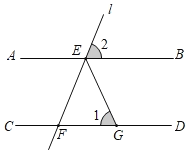
A.30�㣬110��B.56�㣬70��C.70�㣬40��D.100�㣬40��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com