
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的动点,且
上的动点,且![]() ,点
,点![]() 关于
关于![]() 的对称点
的对称点![]() 恰好落在
恰好落在![]() 的内角平分线上,则
的内角平分线上,则![]() 长为_______________.
长为_______________.

【答案】3或![]()
【解析】
此题分两种情况:当D点落在∠A的平分线上时,根据角平分线性质特点得DN=DM,进而得出点C,D,N在同一条直线上,再根据已知条件求出CN,证明△MCD![]() △CAN,根据相似比求出CD即可;当D点落在∠B的平分线上时,同理证明出△MCD
△CAN,根据相似比求出CD即可;当D点落在∠B的平分线上时,同理证明出△MCD![]() △NCB,根据相似比求CD.
△NCB,根据相似比求CD.
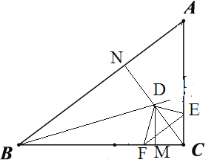
当D点落在∠A的平分线上时,如图:

过点D作DN⊥AB,DM⊥AC,
∵AD平分∠BAC,
∴DN=DM,
由对称知识知CD⊥EF,
∵ ![]() ,DN⊥AB,
,DN⊥AB,
∴点C,D,N在同一条直线上,
∵![]() ,
,![]() ,
,![]() ,
,
∴AB=10,
∵![]() 即
即![]() ,
,
∴CN=4.8,
∴AN=![]() =3.6,
=3.6,
∴ DN=DM=4.8-CD,
∵∠CMD=∠ANC,∠MCD=∠CAN,
∴△MCD![]() △CAN,
△CAN,
∴![]() ,
,
即![]() ,
,
解得:CD=3;
当D点落在∠B的平分线上时,如图:
同理:△MCD![]() △NCB,
△NCB,
∴![]()
∴![]() ,
,
即![]() ,
,
解得:CD=![]() ,
,
故答案为:3或![]() .
.


科目:初中数学 来源: 题型:
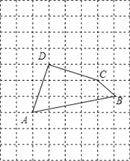
【题目】如图,将四边形ABCD放在每个小正方形的边长为1的网格中,点A.B、C、D均落在格点上.
(Ⅰ)计算AD2+DC2+CB2的值等于_____;
(Ⅱ)请在如图所示的网格中,用无刻度的直尺,画出一个以AB为一边的矩形,使该矩形的面积等于AD2+DC2+CB2,并简要说明画图方法(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
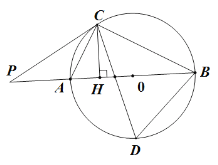
【题目】如图,AB是△ABC外接圆的直径,O为圆心,CHAB,垂足为H,且∠PCA=∠ACH, CD平分∠ACB,交⊙O于点D,连接BD,AP=2.
(1)判断直线PC是否为⊙O的切线,并说明理由;
(2)若∠P=30°,求AC、BC、BD的长.
(3)若tan∠ACP=![]() ,求⊙O半径.
,求⊙O半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形![]() 中,对角线
中,对角线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 以
以![]() 的速度向点
的速度向点![]() 运动,同时动点
运动,同时动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 以
以![]() 支向点
支向点![]() 运动,当其中一个动点停止时另一个动点也随之停止,设运动时间为
运动,当其中一个动点停止时另一个动点也随之停止,设运动时间为![]() (单位:
(单位:![]() )(
)(![]() ),以点
),以点![]() 为圆心,
为圆心,![]() 长为半径的⊙M与射线
长为半径的⊙M与射线![]() 、线段
、线段![]() 分别交于点
分别交于点![]() 、
、![]() ,连接
,连接![]() .
.
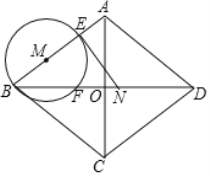
(1)求![]() 的长(用含有
的长(用含有![]() 的代数式表示),并求出
的代数式表示),并求出![]() 的取值范围;
的取值范围;
(2)当![]() 为何值时,线段
为何值时,线段![]() 与⊙M相切?
与⊙M相切?
(3)若⊙M与线段![]() 只有一个公共点,求
只有一个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边上的中线,点
边上的中线,点![]() 为线段
为线段![]() 上一点(不与点
上一点(不与点![]() 、点
、点![]() 重合),连接
重合),连接![]() ,作
,作![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,与
,与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
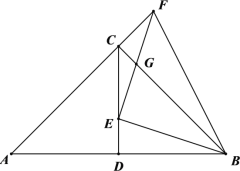
(1)求证:![]() ;
;
(2)求![]() 的度数;
的度数;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 内接于
内接于![]() ,
,![]() 为劣弧
为劣弧![]() 的中点,
的中点,![]() .
.
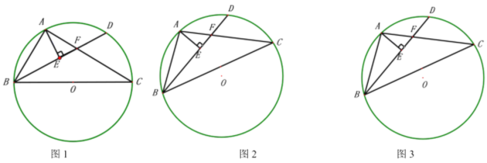
(1)如图1,当![]() 为
为![]() 的直径时,求证:
的直径时,求证:![]() ;
;
(2)如图2,当![]() 不是
不是![]() 的直径,且
的直径,且![]() 时,求证:
时,求证:![]() ;
;
(3)如图3在(2)的条件下,![]() ,
,![]() ,求
,求![]() 长.
长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,等边△ABC,点 E 在 BA 的延长线上,点 D 在 BC 上,且 ED=EC.
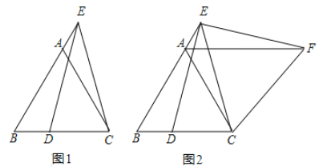
(1)如图 1,求证:AE=DB;
(2)如图 2,将△BCE 绕点 C 顺时针旋转 60°至△ACF(点 B、E 的对应点分别为点 A、F),连接 EF.在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对线段长度之差等于 AB 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=3,点E为对角线AC上一点,EF⊥DE交AB于F,若四边形AFED的面积为4,则四边形AFED的周长为______.
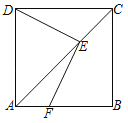
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com