
【题目】已知,等边△ABC,点 E 在 BA 的延长线上,点 D 在 BC 上,且 ED=EC.
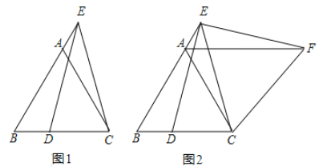
(1)如图 1,求证:AE=DB;
(2)如图 2,将△BCE 绕点 C 顺时针旋转 60°至△ACF(点 B、E 的对应点分别为点 A、F),连接 EF.在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对线段长度之差等于 AB 的长.
【答案】(1)见解析;(2)![]() ;
;![]() ;
;![]() ;
;![]() .
.
【解析】
(1)在BA上截取BF=BD,连接DF,根据等边三角形的性质可得∠BAC=∠B=∠ACB=60°,从而证出△BDF为等边三角形,然后利用AAS证出△CEA≌△EDF,从而得出AE=DF,即可证出结论;
(2)根据图形、全等三角形的性质、旋转的性质和等量代换即可得出结论.
解:(1)在BA上截取BF=BD,连接DF
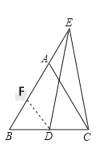
∵△ABC是等边三角形
∴∠BAC=∠B=∠ACB=60°,
∵BF=BD,
∴△BDF为等边三角形
∴BD=DF,∠BFD=∠FDB=60°
∴∠BFD=∠BAC
∴FD∥AC
∴∠EAC=∠DFE
∵ED=EC
∴∠EDC=∠ECD
∵∠EDC+∠EDF=180°-∠FDB=120°,∠ECD+∠CEA=180°-∠B=120°
∴∠CEA=∠EDF
在△CEA和△EDF中
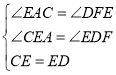
∴△CEA≌△EDF
∴AE=DF
∴AE=DB
(2)由图可知:![]()
∵AE=DB
∴![]()
由旋转的性质可得:BE=AF
∴![]()
∴![]()


科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有![]() 个白球,
个白球,![]() 个黑球和若干个红球,它们除颜色外其余都相同,从中任意摸出
个黑球和若干个红球,它们除颜色外其余都相同,从中任意摸出![]() 个球,是白球的概率为
个球,是白球的概率为![]() .
.
(1)布袋里红球的个数_______;
(2)小亮和小丽将布袋中的白球取出![]() 个,利用剩下的球进行摸球游戏,他们约定:先摸出
个,利用剩下的球进行摸球游戏,他们约定:先摸出![]() 个球后不放回,再摸出
个球后不放回,再摸出![]() 个球,若两个球中有红球则小亮胜,否则小丽胜,你认为这个游戏公平吗?请用列表或画树状图说明理由.
个球,若两个球中有红球则小亮胜,否则小丽胜,你认为这个游戏公平吗?请用列表或画树状图说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小元步行从家去火车站,走到 6 分钟时,以同样的速度回家取物品,然后从家乘出租车赶往火车站,结果比预计步行时间提前了3 分钟.小元离家路程S(米)与时间t(分钟)之间的函数图象如图,从家到火车站路程是( )

A.1300 米B.1400 米C.1600 米D.1500 米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七、八年级各有300名学生,近期对他们“2020年新型冠状病毒”防治知识进行了线上测试,为了了解他们的掌握情况,从七、八年级各随机抽取了50名学生的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息:
a.七年级的频数分布直方图如下(数据分为5组:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100):

b.七年级学生成绩在80≤x<90的这一组是:
80 80.5 81 82 82 83 83.5 84
84 85 86 86.5 87 88 89 89
c.七、八年级学生成绩的平均数、中位数、众数如下:
年级 | 平均数 | 中位数 | 众数 |
七年级 | 85.3 | m | 90 |
八年级 | 87.2 | 85 | 91 |
根据以上信息,回答下列问题:
(1)表中m的值为 ;
(2)在随机抽样的学生中,防治知识成绩为84分的学生,在 年级排名更靠前,理由是 ;
(3)若各年级防治知识的前90名将参加线上防治知识竞赛,预估七年级分数至少达到 分的学生才能入选;
(4)若85分及以上为“优秀”,请估计七年级达到“优秀”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学著作(九章算术)中有如下问题:“今有人持金出五关,前关二而税一.次关三而税一,次关四而税一,次关五而税一,次关六而税一,并五关所税,适重一斤.”其意思为“今有人持金出五关,第![]() 关所收税金为持金的
关所收税金为持金的![]() ,第
,第![]() 关所收税金为剩余金的
关所收税金为剩余金的![]() ,第
,第![]() 关所收税金为剩余金的
关所收税金为剩余金的![]() ,第
,第![]() 关所收税金为剩余金的
关所收税金为剩余金的![]() ,第
,第![]() 关所收税金为剩余金的
关所收税金为剩余金的![]() ,
,![]() 关所收税金之和,恰好重
关所收税金之和,恰好重![]() 斤.”若设这个人原本持金
斤.”若设这个人原本持金![]() 斤,根据题意可列方程为__________ .
斤,根据题意可列方程为__________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,点E是直线AB上的点,过点E的直线l交直线CD于点F,EG平分∠BEF交CD于点G.在直线l绕点E旋转的过程中,图中∠1,∠2的度数可以分别是( )
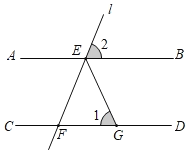
A.30°,110°B.56°,70°C.70°,40°D.100°,40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:
数学活动课上,李老师给出如下定义:如果一个三角形有一边上的中线等于这条边的一半,那么称这个三角形为“智慧三角形”.
理解:
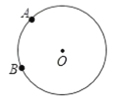
(1)如图,已知![]() 、
、![]() 是
是![]() 上两点,请在圆上找出满足条件的点
上两点,请在圆上找出满足条件的点![]() ,使
,使![]() 为“智慧三角形”(画出点
为“智慧三角形”(画出点![]() 的位置,保留作图痕迹);
的位置,保留作图痕迹);
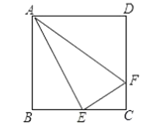
(2)如图,在正方形![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 上一点,且
上一点,且![]() ,试判断
,试判断![]() 是否为“智慧三角形”,并说明理由;
是否为“智慧三角形”,并说明理由;
运用:
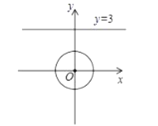
(3)如图,在平面直角坐标系![]() 中,
中,![]() 的半径为1,点
的半径为1,点![]() 是直线
是直线![]() 上的一点,若在
上的一点,若在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 为“智慧三角形”,当其面积取得最小值时,直接写出此时点
为“智慧三角形”,当其面积取得最小值时,直接写出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com