
【题目】如图,AB∥CD,点E是直线AB上的点,过点E的直线l交直线CD于点F,EG平分∠BEF交CD于点G.在直线l绕点E旋转的过程中,图中∠1,∠2的度数可以分别是( )
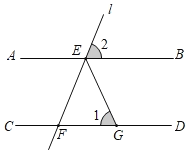
A.30°,110°B.56°,70°C.70°,40°D.100°,40°
【答案】C
【解析】
根据两直线平行,内错角相等可得∠BEG,根据角平分线的定义得到∠BEF,根据邻补角互补求出∠2即可求解.
解:A、∵AB∥CD,
∴∠BEG=∠1=30°,
∵EG平分∠BEF,
∴∠BEF=2∠BEG=60°.
∴∠2=180°﹣∠BEF=120°,不符合题意;
B、∵AB∥CD,
∴∠BEG=∠1=56°,
∵EG平分∠BEF,
∴∠BEF=2∠BEG=112°.
∴∠2=180°﹣∠BEF=68°,不符合题意;
C、∵AB∥CD,
∴∠BEG=∠1=70°,
∵EG平分∠BEF,
∴∠BEF=2∠BEG=140°.
∴∠2=180°﹣∠BEF=40°,符合题意;
D、∵AB∥CD,
∴∠BEG=∠1=100°,
∵EG平分∠BEF,
∴∠BEF=2∠BEG=200°.
∴∠2=360°﹣∠BEF=160°,不符合题意.
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,菱形![]() 中,对角线
中,对角线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 以
以![]() 的速度向点
的速度向点![]() 运动,同时动点
运动,同时动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 以
以![]() 支向点
支向点![]() 运动,当其中一个动点停止时另一个动点也随之停止,设运动时间为
运动,当其中一个动点停止时另一个动点也随之停止,设运动时间为![]() (单位:
(单位:![]() )(
)(![]() ),以点
),以点![]() 为圆心,
为圆心,![]() 长为半径的⊙M与射线
长为半径的⊙M与射线![]() 、线段
、线段![]() 分别交于点
分别交于点![]() 、
、![]() ,连接
,连接![]() .
.
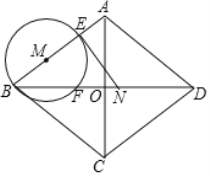
(1)求![]() 的长(用含有
的长(用含有![]() 的代数式表示),并求出
的代数式表示),并求出![]() 的取值范围;
的取值范围;
(2)当![]() 为何值时,线段
为何值时,线段![]() 与⊙M相切?
与⊙M相切?
(3)若⊙M与线段![]() 只有一个公共点,求
只有一个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,等边△ABC,点 E 在 BA 的延长线上,点 D 在 BC 上,且 ED=EC.
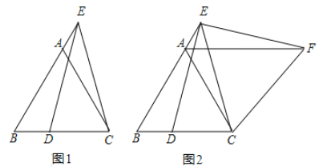
(1)如图 1,求证:AE=DB;
(2)如图 2,将△BCE 绕点 C 顺时针旋转 60°至△ACF(点 B、E 的对应点分别为点 A、F),连接 EF.在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对线段长度之差等于 AB 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
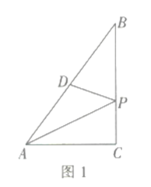
【题目】如图1,在![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 是
是![]() 边上一动点,连接
边上一动点,连接![]() .若
.若![]() 设
设 ![]() (当点
(当点![]() 与点
与点![]() 重合时,
重合时,![]() 的值为
的值为![]() ),
),![]() .
.
小明根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整.
![]() 通过取点、画图、计算,得到了
通过取点、画图、计算,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
说明:补全表格时,相关数值保留一位小数.
(参考数据:![]() ) .
) .
![]() 如图2,描出剩余的点,并用光滑的曲线画出该函数的图象.
如图2,描出剩余的点,并用光滑的曲线画出该函数的图象.
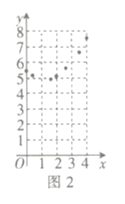
![]() 观察图象,下列结论正确的有 _ .
观察图象,下列结论正确的有 _ .
①函数有最小值,没有最大值
②函数有最小值,也有最大值
③当![]() 时,
时,![]() 随着
随着![]() 的增大而增大
的增大而增大
④当![]() 时,
时,![]() 随着
随着![]() 的增大而减小
的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
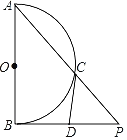
【题目】如图,已知AB为半圆O的直径,过点B作PB⊥OB,连接AP交半圆O于点C,D为BP上一点,CD是半圆O的切线.
(1)求证:CD=DP.
(2)已知半圆O的直径为![]() ,PC=1,求CD的长.
,PC=1,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:⊙O的两条弦![]() ,
,![]() 相交于点
相交于点![]() ,且
,且![]() .
.
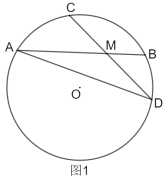
(1)如图1,连接![]() ,求证:
,求证:![]() .
.
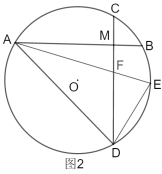
(2)如图2,在![]() ,在
,在![]() 上取一点
上取一点![]() ,使得
,使得![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
①判断![]() 与
与![]() 是否相等,并说明理由.
是否相等,并说明理由.
②若![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
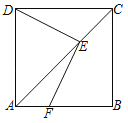
【题目】如图,正方形ABCD中,AB=3,点E为对角线AC上一点,EF⊥DE交AB于F,若四边形AFED的面积为4,则四边形AFED的周长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CA=8,CB=6,动点P从C出发沿CA方向,以每秒1个单位长度的速度向A点匀速运动,到达A点后立即以原来速度沿AC返回;同时动点Q从点A出发沿AB以每秒1个单位长度向点B匀速运动,当Q到达B时,P、Q两点同时停止运动.设P、Q运动的时间为t秒(t>0).
(1)当t为何值时,PQ∥CB?
(2)在点P从C向A运动的过程中,在CB上是否存在点E使△CEP与△PQA全等?若存在,求出CE的长;若不存在,请说明理由;
(3)伴随着P、Q两点的运动,线段PQ的垂直平分线DF交PQ于点D,交折线QB﹣BC﹣CP于点F.当DF经过点C时,求出t的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com