
ЁОЬтФПЁПШчЭМ1ЃЌдк![]() жаЃЌ
жаЃЌ![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЪЧ
ЪЧ![]() БпЩЯвЛЖЏЕуЃЌСЌНг
БпЩЯвЛЖЏЕуЃЌСЌНг![]() ЃЎШє
ЃЎШє![]() Щш
Щш ![]() (ЕБЕу
(ЕБЕу![]() гыЕу
гыЕу![]() жиКЯЪБЃЌ
жиКЯЪБЃЌ![]() ЕФжЕЮЊ
ЕФжЕЮЊ![]() )ЃЌ
)ЃЌ![]() ЃЎ
ЃЎ
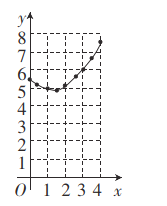
аЁУїИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдКЏЪ§![]() ЫцздБфСП
ЫцздБфСП![]() ЕФБфЛЏЖјБфЛЏЕФЙцТЩНјааСЫЬНОПЃЎ
ЕФБфЛЏЖјБфЛЏЕФЙцТЩНјааСЫЬНОПЃЎ
ЯТУцЪЧаЁУїЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећЃЎ
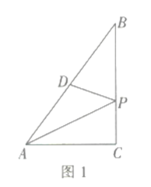
![]() ЭЈЙ§ШЁЕуЁЂЛЭМЁЂМЦЫуЃЌЕУЕНСЫ
ЭЈЙ§ШЁЕуЁЂЛЭМЁЂМЦЫуЃЌЕУЕНСЫ![]() гы
гы![]() ЕФМИзщжЕЃЌШчЯТБэЃК
ЕФМИзщжЕЃЌШчЯТБэЃК
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЫЕУїЃКВЙШЋБэИёЪБЃЌЯрЙиЪ§жЕБЃСєвЛЮЛаЁЪ§ЃЎ
(ВЮПМЪ§ОнЃК![]() ) ЃЎ
) ЃЎ
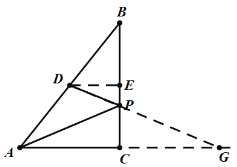
![]() ШчЭМ2ЃЌУшГіЪЃгрЕФЕуЃЌВЂгУЙтЛЌЕФЧњЯпЛГіИУКЏЪ§ЕФЭМЯѓЃЎ
ШчЭМ2ЃЌУшГіЪЃгрЕФЕуЃЌВЂгУЙтЛЌЕФЧњЯпЛГіИУКЏЪ§ЕФЭМЯѓЃЎ
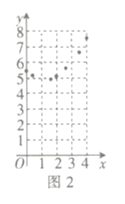
![]() ЙлВьЭМЯѓЃЌЯТСаНсТле§ШЗЕФга _ ЃЎ
ЙлВьЭМЯѓЃЌЯТСаНсТле§ШЗЕФга _ ЃЎ
ЂйКЏЪ§газюаЁжЕЃЌУЛгазюДѓжЕ
ЂкКЏЪ§газюаЁжЕЃЌвВгазюДѓжЕ
ЂлЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЫцзХ
ЫцзХ![]() ЕФдіДѓЖјдіДѓ
ЕФдіДѓЖјдіДѓ
ЂмЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЫцзХ
ЫцзХ![]() ЕФдіДѓЖјМѕаЁ
ЕФдіДѓЖјМѕаЁ
ЁОД№АИЁПЃЈ1ЃЉ5.0ЃЛ6.0ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉЂкЂлЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЙ§ЕуDзїDEЁЭBCЃЌдђDE=![]() ЃЌгЩЙДЙЩЖЈРэЧѓГіPAКЭPDЕФГЄЖШЃЌМДПЩЕУЕНД№АИЃЛ
ЃЌгЩЙДЙЩЖЈРэЧѓГіPAКЭPDЕФГЄЖШЃЌМДПЩЕУЕНД№АИЃЛ
ЃЈ2ЃЉИљОнЬтвтЃЌЭЈЙ§УшЕуЁЂСЌЯпЃЌВЙШЋКЏЪ§ЭМЯёМДПЩЃЛ
ЃЈ3ЃЉНсКЯКЏЪ§ЭМЯёЃЌЗжБ№ЖдЫФИібЁЯюНјааХаЖЯЃЌМДПЩЕУЕНД№АИЃЎ
НтЃКЃЈ1ЃЉЕБ![]() ЪБЃЌШчЭМЃК
ЪБЃЌШчЭМЃК
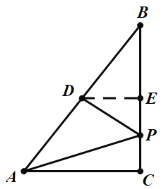
ЁпAC=3ЃЌPC=1ЃЌгЩЙДЙЩЖЈРэЃЌЕУ
![]() ЃЌ
ЃЌ
ЁпЕуDЪЧABжаЕуЃЌDEЁЭBCЃЌЁЯACB=90ЁуЃЌ
ЁрDEЪЧжаЮЛЯпЃЌ
ЁрDE=![]() ЃЌCE=2ЃЌ
ЃЌCE=2ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЛ
ЃЛ
ЕБPC=3ЪБЃЌДЫЪБPE=1ЃЌШчЭМЃК
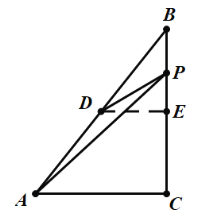
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЛ
ЃЛ
ЙЪД№АИЮЊЃК![]() ЃЛ
ЃЛ![]() ЃЎ
ЃЎ
![]() УшЕуЁЂСЌЯпЃЌШчЭМЃК
УшЕуЁЂСЌЯпЃЌШчЭМЃК
ЃЈ3ЃЉгЩЃЈ2ЃЉжаЭМЯёПЩжЊЃК
КЏЪ§газюаЁжЕЃЌвВгазюДѓжЕЃЛЙЪЂйДэЮѓЃЌЂке§ШЗЃЛ
зїЕуAЙигкBCЕФЖдГЦЕуGЃЌСЌНгDGЃЌгыBCЯрНЛгкЕуPЃЌ
дђДЫЪБPA+PD=DGЮЊзюаЁжЕЃЛШчЭМЃК
ЁпDEЁЮAGЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЕБ![]() ЪБЃЌPA+PD=DGгазюаЁжЕЃЛ
ЪБЃЌPA+PD=DGгазюаЁжЕЃЛ
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЫцзХ
ЫцзХ![]() ЕФдіДѓЖјдіДѓЃЌЂле§ШЗЃЛ
ЕФдіДѓЖјдіДѓЃЌЂле§ШЗЃЛ
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЫцзХ
ЫцзХ![]() ЕФдіДѓЖјМѕаЁЃЌЙЪЂмДэЮѓЃЛ
ЕФдіДѓЖјМѕаЁЃЌЙЪЂмДэЮѓЃЛ
ЙЪД№АИЮЊЃКЂкЂлЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
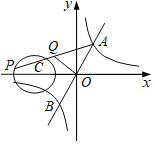
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§y=2xгыЗДБШР§КЏЪ§y=![]() ЃЈkЃО0ЃЉЕФЭМЯѓНЛгкAЃЌBСНЕуЃЌЕуPдквдCЃЈЉ2ЃЌ0ЃЉЮЊдВаФЃЌ1ЮЊАыОЖЕФЁбCЩЯЃЌQЪЧAPЕФжаЕуЃЌвбжЊOQГЄЕФзюДѓжЕЮЊ
ЃЈkЃО0ЃЉЕФЭМЯѓНЛгкAЃЌBСНЕуЃЌЕуPдквдCЃЈЉ2ЃЌ0ЃЉЮЊдВаФЃЌ1ЮЊАыОЖЕФЁбCЩЯЃЌQЪЧAPЕФжаЕуЃЌвбжЊOQГЄЕФзюДѓжЕЮЊ![]() ЃЌдђkЕФжЕЮЊЃЈЁЁЁЁЃЉ
ЃЌдђkЕФжЕЮЊЃЈЁЁЁЁЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіВЛЭИУїЕФВМДќРязАга![]() ИіАзЧђЃЌ
ИіАзЧђЃЌ![]() ИіКкЧђКЭШєИЩИіКьЧђЃЌЫќУЧГ§беЩЋЭтЦфгрЖМЯрЭЌЃЌДгжаШЮвтУўГі
ИіКкЧђКЭШєИЩИіКьЧђЃЌЫќУЧГ§беЩЋЭтЦфгрЖМЯрЭЌЃЌДгжаШЮвтУўГі![]() ИіЧђЃЌЪЧАзЧђЕФИХТЪЮЊ
ИіЧђЃЌЪЧАзЧђЕФИХТЪЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉВМДќРяКьЧђЕФИіЪ§_______ЃЛ
ЃЈ2ЃЉаЁССКЭаЁРіНЋВМДќжаЕФАзЧђШЁГі![]() ИіЃЌРћгУЪЃЯТЕФЧђНјааУўЧђгЮЯЗЃЌЫћУЧдМЖЈЃКЯШУўГі
ИіЃЌРћгУЪЃЯТЕФЧђНјааУўЧђгЮЯЗЃЌЫћУЧдМЖЈЃКЯШУўГі![]() ИіЧђКѓВЛЗХЛиЃЌдйУўГі
ИіЧђКѓВЛЗХЛиЃЌдйУўГі![]() ИіЧђЃЌШєСНИіЧђжагаКьЧђдђаЁССЪЄЃЌЗёдђаЁРіЪЄЃЌФуШЯЮЊетИігЮЯЗЙЋЦНТ№ЃПЧыгУСаБэЛђЛЪїзДЭМЫЕУїРэгЩЃЎ
ИіЧђЃЌШєСНИіЧђжагаКьЧђдђаЁССЪЄЃЌЗёдђаЁРіЪЄЃЌФуШЯЮЊетИігЮЯЗЙЋЦНТ№ЃПЧыгУСаБэЛђЛЪїзДЭМЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЦпЁЂАЫФъМЖИїга300УћбЇЩњЃЌНќЦкЖдЫћУЧЁА2020ФъаТаЭЙкзДВЁЖОЁБЗРжЮжЊЪЖНјааСЫЯпЩЯВтЪдЃЌЮЊСЫСЫНтЫћУЧЕФеЦЮеЧщПіЃЌДгЦпЁЂАЫФъМЖИїЫцЛњГщШЁСЫ50УћбЇЩњЕФГЩМЈЃЈАйЗжжЦЃЉЃЌВЂЖдЪ§ОнЃЈГЩМЈЃЉНјааећРэЁЂУшЪіКЭЗжЮіЃЎЯТУцИјГіСЫВПЗжаХЯЂЃК
aЃЎЦпФъМЖЕФЦЕЪ§ЗжВМжБЗНЭМШчЯТЃЈЪ§ОнЗжЮЊ5зщЃК50ЁмxЃМ60ЃЌ60ЁмxЃМ70ЃЌ70ЁмxЃМ80ЃЌ80ЁмxЃМ90ЃЌ90ЁмxЁм100ЃЉЃК

bЃЎЦпФъМЖбЇЩњГЩМЈдк80ЁмxЃМ90ЕФетвЛзщЪЧЃК
80 80.5 81 82 82 83 83.5 84
84 85 86 86.5 87 88 89 89
cЃЎЦпЁЂАЫФъМЖбЇЩњГЩМЈЕФЦНОљЪ§ЁЂжаЮЛЪ§ЁЂжкЪ§ШчЯТЃК
ФъМЖ | ЦНОљЪ§ | жаЮЛЪ§ | жкЪ§ |
ЦпФъМЖ | 85.3 | m | 90 |
АЫФъМЖ | 87.2 | 85 | 91 |
ИљОнвдЩЯаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉБэжаmЕФжЕЮЊ ЃЛ
ЃЈ2ЃЉдкЫцЛњГщбљЕФбЇЩњжаЃЌЗРжЮжЊЪЖГЩМЈЮЊ84ЗжЕФбЇЩњЃЌдк ФъМЖХХУћИќППЧАЃЌРэгЩЪЧ ЃЛ
ЃЈ3ЃЉШєИїФъМЖЗРжЮжЊЪЖЕФЧА90УћНЋВЮМгЯпЩЯЗРжЮжЊЪЖОКШќЃЌдЄЙРЦпФъМЖЗжЪ§жСЩйДяЕН ЗжЕФбЇЩњВХФмШыбЁЃЛ
ЃЈ4ЃЉШє85ЗжМАвдЩЯЮЊЁАгХауЁБЃЌЧыЙРМЦЦпФъМЖДяЕНЁАгХауЁБЕФШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвЙњЙХДњЪ§бЇжјзї(ОХеТЫуЪѕ)жагаШчЯТЮЪЬтЃКЁАНёгаШЫГжН№ГіЮхЙиЃЌЧАЙиЖўЖјЫАвЛЃЎДЮЙиШ§ЖјЫАвЛЃЌДЮЙиЫФЖјЫАвЛЃЌДЮЙиЮхЖјЫАвЛЃЌДЮЙиСљЖјЫАвЛЃЌВЂЮхЙиЫљЫАЃЌЪЪживЛНяЃЎЁБЦфвтЫМЮЊЁАНёгаШЫГжН№ГіЮхЙиЃЌЕк![]() ЙиЫљЪеЫАН№ЮЊГжН№ЕФ
ЙиЫљЪеЫАН№ЮЊГжН№ЕФ![]() ЃЌЕк
ЃЌЕк![]() ЙиЫљЪеЫАН№ЮЊЪЃгрН№ЕФ
ЙиЫљЪеЫАН№ЮЊЪЃгрН№ЕФ![]() ЃЌЕк
ЃЌЕк![]() ЙиЫљЪеЫАН№ЮЊЪЃгрН№ЕФ
ЙиЫљЪеЫАН№ЮЊЪЃгрН№ЕФ![]() ЃЌЕк
ЃЌЕк![]() ЙиЫљЪеЫАН№ЮЊЪЃгрН№ЕФ
ЙиЫљЪеЫАН№ЮЊЪЃгрН№ЕФ![]() ЃЌЕк
ЃЌЕк![]() ЙиЫљЪеЫАН№ЮЊЪЃгрН№ЕФ
ЙиЫљЪеЫАН№ЮЊЪЃгрН№ЕФ![]() ЃЌ
ЃЌ![]() ЙиЫљЪеЫАН№жЎКЭЃЌЧЁКУжи
ЙиЫљЪеЫАН№жЎКЭЃЌЧЁКУжи![]() НяЃЎЁБШєЩшетИіШЫдБОГжН№
НяЃЎЁБШєЩшетИіШЫдБОГжН№![]() НяЃЌИљОнЬтвтПЩСаЗНГЬЮЊ__________ ЃЎ
НяЃЌИљОнЬтвтПЩСаЗНГЬЮЊ__________ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЭјИёжНжаЃЌ![]() ЁЂ
ЁЂ![]() ЖМЪЧИёЕуЃЌвд
ЖМЪЧИёЕуЃЌвд![]() ЮЊдВаФЃЌ
ЮЊдВаФЃЌ![]() ЮЊАыОЖзїдВЃЌгУЮоПЬЖШЕФжБГпЭъГЩвдЯТЛЭМЃКЃЈВЛаДЛЗЈЃЉ
ЮЊАыОЖзїдВЃЌгУЮоПЬЖШЕФжБГпЭъГЩвдЯТЛЭМЃКЃЈВЛаДЛЗЈЃЉ
ЃЈ1ЃЉдкдВЂйжаЛдВ![]() ЕФвЛИіФкНге§СљБпаЮ
ЕФвЛИіФкНге§СљБпаЮ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉдкЭМЂкжаЛдВ![]() ЕФвЛИіФкНге§АЫБпаЮ
ЕФвЛИіФкНге§АЫБпаЮ![]() .
.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЁЮCDЃЌЕуEЪЧжБЯпABЩЯЕФЕуЃЌЙ§ЕуEЕФжБЯпlНЛжБЯпCDгкЕуFЃЌEGЦНЗжЁЯBEFНЛCDгкЕуGЃЎдкжБЯпlШЦЕуEа§зЊЕФЙ§ГЬжаЃЌЭМжаЁЯ1ЃЌЁЯ2ЕФЖШЪ§ПЩвдЗжБ№ЪЧЃЈ ЃЉ
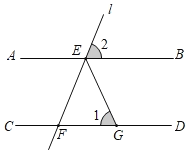
A.30ЁуЃЌ110ЁуB.56ЁуЃЌ70ЁуC.70ЁуЃЌ40ЁуD.100ЁуЃЌ40Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌХзЮяЯп
жаЃЌХзЮяЯп![]() гы
гы![]() жсНЛгкЕуAЃЌНЋЕуAЯђгвЦНвЦ2ИіЕЅЮЛГЄЖШЃЌЕУЕНЕуBЃЌЕуBдкХзЮяЯпЩЯЃЎ
жсНЛгкЕуAЃЌНЋЕуAЯђгвЦНвЦ2ИіЕЅЮЛГЄЖШЃЌЕУЕНЕуBЃЌЕуBдкХзЮяЯпЩЯЃЎ
ЃЈ1ЃЉЧѓЕуBЕФзјБъЃЈгУКЌ![]() ЕФЪНзгБэЪОЃЉЃЛ
ЕФЪНзгБэЪОЃЉЃЛ
ЃЈ2ЃЉЧѓХзЮяЯпЕФЖдГЦжсЃЛ
ЃЈ3ЃЉвбжЊЕу![]() ЃЌ
ЃЌ![]() ЃЎШєХзЮяЯпгыЯпЖЮPQЧЁгавЛИіЙЋЙВЕуЃЌНсКЯКЏЪ§ЭМЯѓЃЌЧѓ
ЃЎШєХзЮяЯпгыЯпЖЮPQЧЁгавЛИіЙЋЙВЕуЃЌНсКЯКЏЪ§ЭМЯѓЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪЋДЪЪЧжаЙњШЫзюОЕфЕФЧщИаБэДяЗНЪНЃЌвВЪЧУёзхЩњДцбгајЕФУќТіЃЎЮЊСЫКыбяЪЋДЪЙњбЇЃЌЮваЃПЊеЙСЫЁАОЕфгНСїДЋЁБЕФЛюЖЏЃЎЧсВІОЕфЕФЧйЯвЃЌЮвУЧНЋЙњМвЁЂУёзхЁЂЮФЛЏЕФУРКУОЋЩёЮФЛЏДЋГаЯТРДЃЌИГгшОЕфЮФЛЏвдЪБДњЕФСщЛъЃЎЯжЮваЃГѕЖўЃЈ1ЃЉАрЮЊВЮМгЁАОЕфгНСїДЋЁБЛюЖЏЃЌАрЮЏЛсзМБИзтСобнГіЗўзАЁЂЙКТђВПЗжЕРОпЙЉАрМЖМЏЬхЪЙгУЃЎ
ЃЈ1ЃЉАрЮЏЛсЭЈЙ§ЖрЗНБШНЯЃЌОіЖЈгУ500дЊдкAЩЬЕъзтСоЗўзАЃЌгУ300дЊдкBЩЬЕъЙКТђЕРОпЃЎвбжЊзтСовЛЬзЗўзАБШЙКТђвЛЬзЕРОпЙѓ30дЊЃЌЭЌЪБЫљашЕРОпБШЫљашЗўзАЖр5ЬзЃЌдђГѕЖўЃЈ1ЃЉАрАрЮЏЛсзтСоСЫЖрЩйЬзбнГіЗўзАЁЂЙКТђСЫЖрЩйЬзЕРОпЃП
ЃЈ2ЃЉвђКѓЦкВЮШќНкФПШЫдБЕФЕїећЃЌашвЊзтСоИќЖрЕФЗўзАЃЌЙКТђИќЖрЕФЕРОпЃЎОГѕВНЭГМЦЃЌзюжеашвЊзтСоЕФбнГіЗўзАЬзЪ§БШЃЈ1ЃЉжаЕФбнГіЗўзАЬзЪ§діМгСЫ5a%ЃЈaЃМ60ЃЉЃЌЕРОпЬзЪ§БШЃЈ1ЃЉжаЕФЕРОпЬзЪ§діМгСЫ2a%ЃЎГѕЖўЃЈ1ЃЉАрАрЮЏЛсашвЊдйДЮзтСоЗўзАКЭЙКТђЕРОпЃЌгжЧАШЅгыAЩЬЕъЁЂBЩЬЕъвщМлЃЌСНИіЩЬЕъЖМдкдРДЕФЪлМлЩЯИјгшСЫa%ЕФгХЛнЃЌетДЮзтСоЗўзАКЭЙКТђЕРОпзмЙВгУСЫ279дЊЃЌЧѓaЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com