
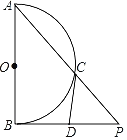
【题目】如图,已知AB为半圆O的直径,过点B作PB⊥OB,连接AP交半圆O于点C,D为BP上一点,CD是半圆O的切线.
(1)求证:CD=DP.
(2)已知半圆O的直径为![]() ,PC=1,求CD的长.
,PC=1,求CD的长.
【答案】(1)证明见解析,(2)CD=![]() .
.
【解析】
(1)如图1(见解析),连接OC,先根据圆的切线的性质得出![]() ,从而可得
,从而可得![]() ,再根据直角三角形的性质可得
,再根据直角三角形的性质可得![]() ,然后根据等腰三角形的性质可得
,然后根据等腰三角形的性质可得![]() ,从而可得
,从而可得![]() ,最后根据等腰三角形的性质即可得证;
,最后根据等腰三角形的性质即可得证;
(2)如图2(见解析),连接OC、BC,先根据圆周角定理得出![]() ,再根据相似三角形的判定与性质可得
,再根据相似三角形的判定与性质可得![]() ,从而可求出
,从而可求出![]() ,然后在
,然后在![]() 中利用勾股定理可求出
中利用勾股定理可求出![]() ,最后根据角的和差、等腰三角形的性质可得
,最后根据角的和差、等腰三角形的性质可得![]() ,结合题(1)的结论可得
,结合题(1)的结论可得![]() ,由此即可得.
,由此即可得.
(1)如图1,连接OC
∵CD是半圆O的切线
∴OC⊥CD,即![]()
∴![]()
∵PB⊥AB
∴![]()
∴![]()
![]()
又![]()
![]()
∴![]()
∴![]() ;
;
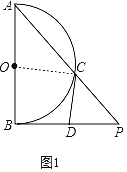
(2)如图2,连接OC、BC
∵AB是半圆O的直径
∴![]() ,
,![]()
∴![]()
又∵![]()
∴![]()
∴![]() ,即
,即![]()
∵![]()
∴![]()
解得![]() 或
或![]() (不符题意,舍去)
(不符题意,舍去)
∴![]()
在![]() 中,
中,![]()
由(1)得![]()
即![]()
∵![]()
∴![]()
∴![]()
∴![]()
由(1)知![]()
∴![]() .
.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:
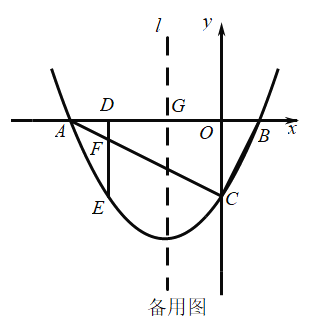
【题目】如图,抛物线![]() 与
与![]() 轴负半轴交于点
轴负半轴交于点![]() ,与
,与![]() 轴正半轴交于点
轴正半轴交于点![]() ,与
,与![]() 轴负半轴交于点
轴负半轴交于点![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求点![]() 的坐标和抛物线的函数关系式;
的坐标和抛物线的函数关系式;
(2)点![]() 是
是![]() 上一点(不与点
上一点(不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线,交抛物线于点
轴的垂线,交抛物线于点![]() ,交
,交![]() 于点
于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)设抛物线的对称轴![]() 交
交![]() 轴于点
轴于点![]() ,在(2)的条件下,点
,在(2)的条件下,点![]() 是抛物线对称轴上一点,点
是抛物线对称轴上一点,点![]() 是坐标平面内一点,是否存在点
是坐标平面内一点,是否存在点![]() 、
、![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,请求出点
为顶点的四边形是菱形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
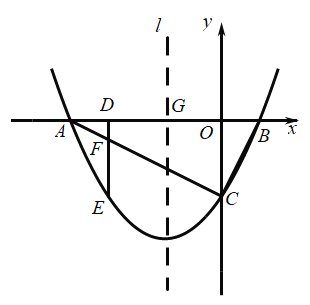
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小元步行从家去火车站,走到 6 分钟时,以同样的速度回家取物品,然后从家乘出租车赶往火车站,结果比预计步行时间提前了3 分钟.小元离家路程S(米)与时间t(分钟)之间的函数图象如图,从家到火车站路程是( )

A.1300 米B.1400 米C.1600 米D.1500 米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学著作(九章算术)中有如下问题:“今有人持金出五关,前关二而税一.次关三而税一,次关四而税一,次关五而税一,次关六而税一,并五关所税,适重一斤.”其意思为“今有人持金出五关,第![]() 关所收税金为持金的
关所收税金为持金的![]() ,第
,第![]() 关所收税金为剩余金的
关所收税金为剩余金的![]() ,第
,第![]() 关所收税金为剩余金的
关所收税金为剩余金的![]() ,第
,第![]() 关所收税金为剩余金的
关所收税金为剩余金的![]() ,第
,第![]() 关所收税金为剩余金的
关所收税金为剩余金的![]() ,
,![]() 关所收税金之和,恰好重
关所收税金之和,恰好重![]() 斤.”若设这个人原本持金
斤.”若设这个人原本持金![]() 斤,根据题意可列方程为__________ .
斤,根据题意可列方程为__________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组对角互补的四边形叫做互补四边形.
![]() 概念理解:
概念理解:
①在互补四边形![]() 中,
中,![]() 与
与![]() 是一组对角,若
是一组对角,若![]() 则
则![]() _
_ ![]()
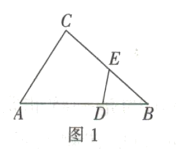
②如图1,在![]() 中,点
中,点![]() 分别在边
分别在边![]() 上,且
上,且![]() 求证:四边形
求证:四边形![]() 是互补四边形.
是互补四边形.
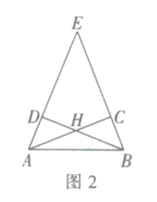
![]() 探究发现:如图2,在等腰
探究发现:如图2,在等腰![]() 中,
中,![]() 点
点![]() 分别在边
分别在边![]() 上,
上, ![]() 四边形
四边形![]() 是互补四边形,求证:
是互补四边形,求证:![]() .
.
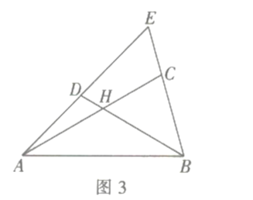
![]() 推广运用:如图3,在
推广运用:如图3,在![]() 中,点
中,点![]() 分别在边
分别在边![]() 上,
上,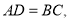 四边形
四边形![]() 是互补四边形,若
是互补四边形,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,点E是直线AB上的点,过点E的直线l交直线CD于点F,EG平分∠BEF交CD于点G.在直线l绕点E旋转的过程中,图中∠1,∠2的度数可以分别是( )
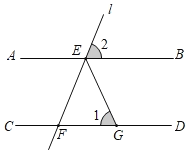
A.30°,110°B.56°,70°C.70°,40°D.100°,40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,折叠矩形![]() ,具体操作:①点
,具体操作:①点![]() 为
为![]() 边上一点(不与
边上一点(不与![]() 、
、![]() 重合),把
重合),把![]() 沿
沿![]() 所在的直线折叠,
所在的直线折叠,![]() 点的对称点为
点的对称点为![]() 点;②过点
点;②过点![]() 对折
对折![]() ,折痕
,折痕![]() 所在的直线交
所在的直线交![]() 于点
于点![]() 、
、![]() 点的对称点为
点的对称点为![]() 点.
点.
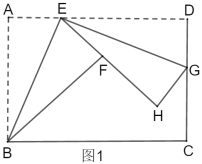
(1)求证:![]() ∽
∽![]() .
.
(2)若![]() ,
,![]() .
.
①点![]() 在移动的过程中,求
在移动的过程中,求![]() 的最大值.
的最大值.
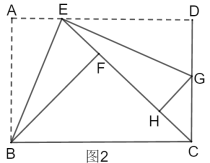
②如图2,若点![]() 恰在直线
恰在直线![]() 上,连接
上,连接![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的网格中,有两个完全相同的直角三角形纸片,如果把其中一个三角形纸片先横向平移![]() 格,再纵向平移
格,再纵向平移![]() 格,就能使它的一条边与另一个三角形纸片的一条边重合,拼接成一个四边形,那么
格,就能使它的一条边与另一个三角形纸片的一条边重合,拼接成一个四边形,那么![]() 的结果( )
的结果( )

A.只有一个确定的值B.有两个不同的值
C.有三个不同的值D.有三个以上不同的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂有甲、乙两台机器加工同一种零件,已知一小时甲加工的零件数与一小时乙加工的零件数的和为36个,甲加工80个零件与乙加工100个零件的所用时间相等.求甲、乙两台机器每小时分别加工零件多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com