
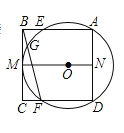
【题目】如图,![]() 过正方形
过正方形![]() 的顶点
的顶点![]() ,且与
,且与![]() 相切于点
相切于点![]() 分别交
分别交![]() 于
于![]() 两点,连接
两点,连接![]() 并延长交
并延长交![]() 于点
于点![]() .
.
(1)求证![]()
(2)连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() 求
求![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据⊙O与BC相切于点M,可得∠BMN=90°,得四边形ABCD是正方形,再根据垂径定理即可证明AN=DN;
(2)解法一:接DE,EF,DG,可得DE是⊙O的直径,且四边形AEFD是矩形,由(1)知四边形ABMN是矩形,设OA=r,则ON=8-r,AN=4,在Rt△AON中,根据勾股定理可得r的值,然后由∠BFE=∠EDG,得sin∠BFE=sin∠EDG,进而可得EG的长;
解法二:连接![]() 由圆周角定理可得
由圆周角定理可得![]() 是
是![]() 的直径,且四边形
的直径,且四边形![]() 是矩形,由(1)知四边形ABMN是矩形,设OA=r,则ON=8-r,AN=4,在Rt△AON中,根据勾股定理可得r的值,由圆内接四边形性质求得
是矩形,由(1)知四边形ABMN是矩形,设OA=r,则ON=8-r,AN=4,在Rt△AON中,根据勾股定理可得r的值,由圆内接四边形性质求得![]() ,从而利用AA定理求得
,从而利用AA定理求得![]() ,从而利用相似三角形的性质列比例式求解即可.
,从而利用相似三角形的性质列比例式求解即可.
解:![]()
![]() 与边
与边![]() 相切与点,
相切与点,![]()
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]()
![]()
由垂径定理得![]()
![]() 解法一:连接
解法一:连接![]()
![]()
![]() ,
,
![]() 是
是![]() 的直径,且四边形
的直径,且四边形![]() 是矩形.
是矩形.
由![]() 知四边形
知四边形![]() 是矩形,
是矩形,
![]()
设![]() ,在
,在![]() 中
中
由勾股定理得![]() ,解得
,解得![]()
![]() ,
,
![]()
![]() ,
,![]()
![]()
![]()
![]()
即![]()
![]()
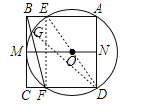
解法二:连接![]()
![]()
![]()
![]() 是
是![]() 的直径,且四边形
的直径,且四边形![]() 是矩形,
是矩形,
由![]() 知四边形
知四边形![]() 是矩形,
是矩形,
![]()
设![]() ,在
,在![]() 中,
中,
由勾股定理得![]() ,解得
,解得![]()
![]()
![]()
![]()
![]()
![]()
![]()
即![]()
![]() .
.



科目:初中数学 来源: 题型:
【题目】已知:点M是平行四边形ABCD对角线AC所在直线上的一个动点(点M不与点A、C重合),分别过点A、C向直线BM作垂线,垂足分别为点E、F,点O为AC的中点.
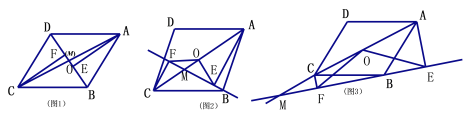
⑴如图1,当点M与点O重合时,OE与OF的数量关系是 .
⑵直线BM绕点B逆时针方向旋转,且∠OFE=30°.
①如图2,当点M在线段AC上时,猜想线段CF、AE、OE之间有怎样的数量关系?请你写出来并加以证明;
②如图3,当点M在线段AC的延长线上时,请直接写出线段CF、AE、OE之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E为BC边上的一点,连接AE,过点D作DM⊥AE,垂足为点M,交AB于点F.将△AMF沿AB翻折得到△ANF.延长DM,AN交于点P. 给出以下结论①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() ,则
,则![]() ;.其中正确的是( )
;.其中正确的是( )
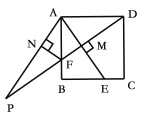
A.①②③④B.①②③C.①②④D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴负半轴交于点
轴负半轴交于点![]() ,与
,与![]() 轴正半轴交于点
轴正半轴交于点![]() ,与
,与![]() 轴负半轴交于点
轴负半轴交于点![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求点![]() 的坐标和抛物线的函数关系式;
的坐标和抛物线的函数关系式;
(2)点![]() 是
是![]() 上一点(不与点
上一点(不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线,交抛物线于点
轴的垂线,交抛物线于点![]() ,交
,交![]() 于点
于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)设抛物线的对称轴![]() 交
交![]() 轴于点
轴于点![]() ,在(2)的条件下,点
,在(2)的条件下,点![]() 是抛物线对称轴上一点,点
是抛物线对称轴上一点,点![]() 是坐标平面内一点,是否存在点
是坐标平面内一点,是否存在点![]() 、
、![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,请求出点
为顶点的四边形是菱形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
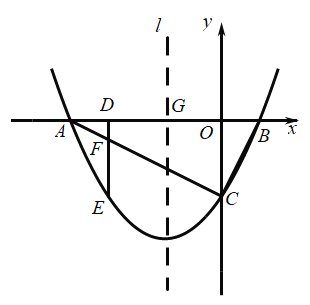
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小元步行从家去火车站,走到 6 分钟时,以同样的速度回家取物品,然后从家乘出租车赶往火车站,结果比预计步行时间提前了3 分钟.小元离家路程S(米)与时间t(分钟)之间的函数图象如图,从家到火车站路程是( )

A.1300 米B.1400 米C.1600 米D.1500 米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,折叠矩形![]() ,具体操作:①点
,具体操作:①点![]() 为
为![]() 边上一点(不与
边上一点(不与![]() 、
、![]() 重合),把
重合),把![]() 沿
沿![]() 所在的直线折叠,
所在的直线折叠,![]() 点的对称点为
点的对称点为![]() 点;②过点
点;②过点![]() 对折
对折![]() ,折痕
,折痕![]() 所在的直线交
所在的直线交![]() 于点
于点![]() 、
、![]() 点的对称点为
点的对称点为![]() 点.
点.
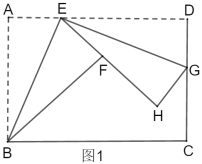
(1)求证:![]() ∽
∽![]() .
.
(2)若![]() ,
,![]() .
.
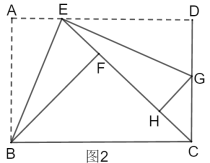
①点![]() 在移动的过程中,求
在移动的过程中,求![]() 的最大值.
的最大值.
②如图2,若点![]() 恰在直线
恰在直线![]() 上,连接
上,连接![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com