
°æƒø°ø“—÷™£∫µ„M «∆Ω––Àƒ±fl–ŒABCD∂‘Ω«œflACÀ˘‘⁄÷±œfl…œµƒ“ª∏ˆ∂ص„£®µ„M≤ª”ε„A°¢C÷ÿ∫œ£©£¨∑÷±π˝µ„A°¢CœÚ÷±œflBM◊˜¥πœfl£¨¥π◊„∑÷±Œ™µ„E°¢F£¨µ„OŒ™ACµƒ÷–µ„£Æ
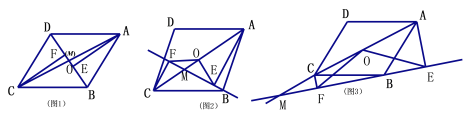
¢≈»ÁÕº1,µ±µ„M”ε„O÷ÿ∫œ ±£¨OE”ÎOFµƒ ˝¡øπÿœµ « £Æ
¢∆÷±œflBM»∆µ„BƒÊ ±’Î∑ΩœÚ–˝◊™£¨«“°œOFE=30°„£Æ
¢Ÿ»ÁÕº2£¨µ±µ„M‘⁄œfl∂ŒAC…œ ±£¨≤¬œÎœfl∂ŒCF°¢AE°¢OE÷ƺ‰”–‘ı—˘µƒ ˝¡øπÿœµ£ø«Îƒ„–¥≥ˆ¿¥≤¢º”“‘÷§√˜£ª
¢⁄»ÁÕº3£¨µ±µ„M‘⁄œfl∂ŒACµƒ—”≥§œfl…œ ±£¨«Î÷±Ω”–¥≥ˆœfl∂ŒCF°¢AE°¢OE÷ƺ‰µƒ ˝¡øπÿœµ£Æ
°æ¥∞∏°ø£®1£©OE=OF£ª£®2£©¢Ÿ![]() £¨œÍº˚Ω‚Œˆ£ª¢⁄CF=OE-AE
£¨œÍº˚Ω‚Œˆ£ª¢⁄CF=OE-AE
°æΩ‚Œˆ°ø
£®1£©”…°˜AOE°’°˜COFº¥ø…µ√≥ˆΩ·¬€£Æ
£®2£©¢ŸÕº2÷–µƒΩ·¬€Œ™£∫CF=OE+AE£¨—”≥§EOΩªCF”⁄µ„N£¨÷ª“™÷§√˜°˜EOA°’°˜NOC£¨°˜OFN «µ»±fl»˝Ω«–Œ£¨º¥ø…Ω‚æˆŒ £Æ
¢⁄Õº3÷–µƒΩ·¬€Œ™£∫CF=OE-AE£¨—”≥§EOΩªFCµƒ—”≥§œfl”⁄µ„G£¨÷§√˜∑Ω∑®¿‡À∆£Æ
Ω‚£∫¢≈°fl ![]()
°‡AE°ŒCF
°‡![]() ”÷
”÷![]() ,OA=OC
,OA=OC
°‡°˜AOE°’°˜COF.
°‡OE=OF£Æ
¢∆¢Ÿ ![]()
—”≥§EOΩªCF—”≥§œfl”⁄N£Æ

°fl ![]()
°‡AE°ŒCF
°‡![]() ”÷
”÷![]() ,OA=OC
,OA=OC
°‡°˜OAE°’°˜OCN
°‡AE=CN,OE=ON ”÷![]() ,
,![]()
°‡OF=ON=OE, ![]()
°‡OF=FN=ON=OE,”÷AE=CN
°‡CF=AE-OE
¢⁄CF=OE-AE,÷§√˜»Áœ¬£∫
—”≥§EOΩªFCµƒ—”≥§œfl”⁄µ„G

°fl ![]()
°‡AE°ŒCF
°‡°œG=°œAEO,°œOCG=°œEA0£¨
”÷°flAO=OC£¨
°‡°˜OAE°’°˜OCG.
°‡AE=CG,OG=OE.
”÷![]() ,
,![]()
°‡OF=OG=OE, ![]()
°‡°˜OGF «µ»±fl»˝Ω«–Œ£¨
°‡FG=OF=OE.
°‡CF=OE-AE.


 √˚–£øŒÃ√œµ¡–¥∞∏
√˚–£øŒÃ√œµ¡–¥∞∏
| ƒÍº∂ | ∏fl÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏fl“ª | ∏fl“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl∂˛ | ∏fl∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl»˝ | ∏fl»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨∂‘”⁄µ„![]() ∫Õ
∫Õ![]() £¨∏¯≥ˆ»Áœ¬∂®“£∫
£¨∏¯≥ˆ»Áœ¬∂®“£∫
»Áπ˚ £¨ƒ«√¥≥∆µ„
£¨ƒ«√¥≥∆µ„![]() Œ™µ„
Œ™µ„![]() µƒ°∞∞ÈÀʵ„°±£Æ
µƒ°∞∞ÈÀʵ„°±£Æ
¿˝»Á£∫µ„![]() µƒ°∞∞ÈÀʵ„°±Œ™µ„
µƒ°∞∞ÈÀʵ„°±Œ™µ„![]() £ªµ„
£ªµ„![]() µƒ°∞∞ÈÀʵ„°±Œ™µ„
µƒ°∞∞ÈÀʵ„°±Œ™µ„![]() £Æ
£Æ
£®1£©÷±Ω”–¥≥ˆµ„![]() µƒ°∞∞ÈÀʵ„°±
µƒ°∞∞ÈÀʵ„°±![]() µƒ◊¯±Í£Æ
µƒ◊¯±Í£Æ
£®2£©µ„![]() ‘⁄∫Ø ˝
‘⁄∫Ø ˝![]() µƒÕºœÛ…œ£¨»Ù∆‰°∞∞ÈÀʵ„°±
µƒÕºœÛ…œ£¨»Ù∆‰°∞∞ÈÀʵ„°±![]() µƒ◊›◊¯±ÍŒ™2£¨«Û∫Ø ˝
µƒ◊›◊¯±ÍŒ™2£¨«Û∫Ø ˝![]() µƒΩ‚Œˆ Ω£Æ
µƒΩ‚Œˆ Ω£Æ
£®3£©µ„![]() ‘⁄∫Ø ˝
‘⁄∫Ø ˝![]() µƒÕºœÛ…œ£¨«“µ„
µƒÕºœÛ…œ£¨«“µ„![]() πÿ”⁄
πÿ”⁄![]() ÷·∂‘≥∆£¨µ„
÷·∂‘≥∆£¨µ„![]() µƒ°∞∞ÈÀʵ„°±Œ™
µƒ°∞∞ÈÀʵ„°±Œ™![]() £Æ»Ùµ„
£Æ»Ùµ„![]() ‘⁄µ⁄“ªœÛœfi£¨«“
‘⁄µ⁄“ªœÛœfi£¨«“![]() £¨«Û¥À ±°∞∞ÈÀʵ„°±
£¨«Û¥À ±°∞∞ÈÀʵ„°±![]() µƒ∫·◊¯±Í£Æ
µƒ∫·◊¯±Í£Æ
£®4£©µ„![]() ‘⁄∫Ø ˝
‘⁄∫Ø ˝![]() µƒÕºœÛ…œ£¨»Ù∆‰°∞∞ÈÀʵ„°±
µƒÕºœÛ…œ£¨»Ù∆‰°∞∞ÈÀʵ„°±![]() µƒ◊›◊¯±Í
µƒ◊›◊¯±Í![]() µƒ◊Ó¥Û÷µŒ™
µƒ◊Ó¥Û÷µŒ™![]() £¨÷±Ω”–¥≥ˆ µ ˝
£¨÷±Ω”–¥≥ˆ µ ˝![]() µƒ»°÷µ∑∂Œß£Æ
µƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥—ß–£Œ™¡ÀΩ‚—ß…˙“fl«È∆⁄º‰“ªÃÏ‘⁄œfl—ßœ∞ ±≥§£¨Ω¯––¡À“ª¥ŒÀʪ˙Œ æ̵˜≤È£®√ø»À÷ªƒ‹—°‘Ò∆‰÷–“ªœÓ£©£¨≤¢Ω´µ˜≤È ˝æ›’˚¿Ì∫ÛªÊ≥…»Áœ¬¡Ω∑˘≤ªÕÍ’˚µƒÕ≥º∆Õº£Æ«Î∏˘æ›Õº÷––≈œ¢Ω‚¥œ¬¡–Œ £∫
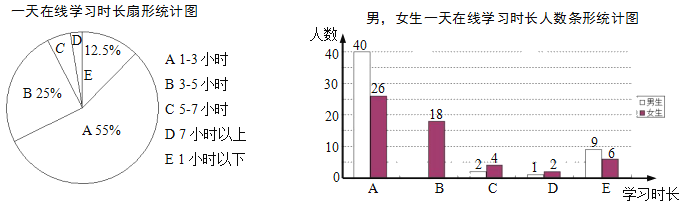
£®1£©«Û≤Œ”ÎŒ æ̵˜≤ȵƒ◊‹»À ˝£Æ
£®2£©≤π»´Ãı–ŒÕ≥º∆Õº£¨≤¢«Û≥ˆ“ªÃÏ‘⁄œfl—ßœ∞°∞5©Å7∏ˆ–° ±°±µƒ…»–Œ‘≤–ƒΩ«∂» ˝£Æ
£®3£©»Ù∏√–£π≤”–—ß…˙1800√˚£¨ ‘π¿º∆»´–£“ªÃÏ‘⁄œfl—ßœ∞°∞7–° ±“‘…œ°±µƒ—ß…˙»À ˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø–°√˜ «“ª√˚Ω°≤Ω◊fl‘À∂صƒ∞Æ∫√’fl£¨À˚”√ ÷ª˙»Ìº˛º«¬º¡ÀÀ˚Ω¸∆⁄Ω°≤Ω◊flµƒ≤Ω ˝£®µ•Œª£∫ÕÚ≤Ω£©£¨ªÊ÷∆≥ˆ»Áœ¬µƒÕ≥º∆Õº¢Ÿ∫ÕÕ≥º∆Õº¢⁄£¨«Î∏˘æ›œ‡πÿ–≈œ¢£¨Ω‚¥œ¬¡–Œ £∫
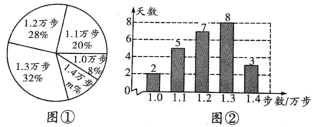
£®¢Ò£©±æ¥Œº«¬ºµƒ◊‹ÃÏ ˝Œ™_____________£¨Õº¢Ÿ÷–mµƒ÷µŒ™______________£ª
£®¢Ú£©«Û–°√˚Ω¸∆⁄Ω°≤Ω◊fl≤Ω ˝µƒ∆Ωæ˘ ˝°¢÷⁄ ˝∫Õ÷–Œª ˝£ª
£®¢Û£©∏˘æ›—˘±æ ˝æ›£¨»Ù–°√˜º·≥÷Ω°≤Ω◊fl“ªƒÍ£®º«Œ™365ÃÏ£©£¨ ‘π¿º∆≤Ω ˝Œ™1.1ÕÚ≤ΩµƒÃÏ ˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨°˜ABCµƒ»˝∏ˆ∂•µ„◊¯±Í∑÷±Œ™A£®3£¨2£©°¢B£®3£¨5£©°¢C£®1£¨2£©£Æ

¢≈‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–ª≠≥ˆ°˜ABCπÿ”⁄‘≠µ„∂‘≥∆µƒ°˜A1B1C1;
¢∆∞—°˜ABC»∆µ„AÀ≥ ±’Ζ˝◊™“ª∂®µƒΩ«∂»£¨µ√Õº÷–µƒ°˜AB2C2£¨µ„C2‘⁄AB…œ£Æ«Î–¥≥ˆ£∫
¢Ÿ–˝◊™Ω«Œ™ ∂»£ª
¢⁄µ„B2µƒ◊¯±ÍŒ™ £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
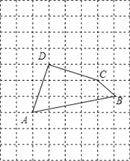
°æƒø°ø»ÁÕº£¨Ω´Àƒ±fl–ŒABCD∑≈‘⁄√ø∏ˆ–°’˝∑Ω–Œµƒ±fl≥§Œ™1µƒÕ¯∏Ò÷–£¨µ„A£ÆB°¢C°¢Dæ˘¬‰‘⁄∏Òµ„…œ£Æ
£®¢Ò£©º∆À„AD2+DC2+CB2µƒ÷µµ»”⁄_____£ª
£®¢Ú£©«Î‘⁄»ÁÕºÀ˘ 浃կ∏Ò÷–£¨”√ŒfiøÃ∂»µƒ÷±≥fl£¨ª≠≥ˆ“ª∏ˆ“‘ABŒ™“ª±flµƒæÿ–Œ£¨ π∏√æÿ–Œµƒ√ʪ˝µ»”⁄AD2+DC2+CB2£¨≤¢ºÚ“™Àµ√˜ª≠Õº∑Ω∑®£®≤ª“™«Û÷§√˜£©£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øæÿ–Œ![]() µƒ¡ΩÃı∂‘≥∆÷·Œ™◊¯±Í÷·£¨µ„
µƒ¡ΩÃı∂‘≥∆÷·Œ™◊¯±Í÷·£¨µ„![]() µƒ◊¯±ÍŒ™
µƒ◊¯±ÍŒ™![]() .“ª’≈Õ∏√˜÷Ω…œª≠”–“ª∏ˆµ„
.“ª’≈Õ∏√˜÷Ω…œª≠”–“ª∏ˆµ„![]() ∫Õ“ªÃı≈◊ŒÔœfl£¨∆Ω“∆Õ∏√˜÷Ω£¨ πµ„
∫Õ“ªÃı≈◊ŒÔœfl£¨∆Ω“∆Õ∏√˜÷Ω£¨ πµ„![]() ”ε„
”ε„![]() ÷ÿ∫œ£¨¥À ±≈◊ŒÔœflµƒ∫Ø ˝±Ì¥Ô ΩŒ™
÷ÿ∫œ£¨¥À ±≈◊ŒÔœflµƒ∫Ø ˝±Ì¥Ô ΩŒ™![]() £¨‘Ÿ¥Œ∆Ω“∆Õ∏√˜÷Ω£¨ πµ„
£¨‘Ÿ¥Œ∆Ω“∆Õ∏√˜÷Ω£¨ πµ„![]() ”ε„
”ε„![]() ÷ÿ∫œ£¨‘Ú∏√≈◊ŒÔœflµƒ∫Ø ˝±Ì¥Ô Ω±‰Œ™_______.
÷ÿ∫œ£¨‘Ú∏√≈◊ŒÔœflµƒ∫Ø ˝±Ì¥Ô Ω±‰Œ™_______.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨![]() «µ»±fl»˝Ω«–Œ£¨µ„
«µ»±fl»˝Ω«–Œ£¨µ„![]() £¨µ„
£¨µ„![]() £¨µ„
£¨µ„![]() «
«![]() ±fl…œµƒ“ª∏ˆ∂ص„£®”ε„
±fl…œµƒ“ª∏ˆ∂ص„£®”ε„![]() °¢
°¢![]() ≤ª÷ÿ∫œ£©.÷±œfl
≤ª÷ÿ∫œ£©.÷±œfl![]() «æ≠π˝µ„
«æ≠π˝µ„![]() µƒ“ªÃı÷±œfl£¨∞—
µƒ“ªÃı÷±œfl£¨∞—![]() —ÿ÷±œfl
—ÿ÷±œfl![]() ’€µ˛£¨µ„
’€µ˛£¨µ„![]() µƒ∂‘”¶µ„ «µ„
µƒ∂‘”¶µ„ «µ„![]() £Æ
£Æ
£®1£©»ÁÕº¢Ÿ£¨µ±![]() ±£¨»Ù÷±œfl
±£¨»Ù÷±œfl![]() £¨«Ûµ„
£¨«Ûµ„![]() µƒ◊¯±Í£ª
µƒ◊¯±Í£ª
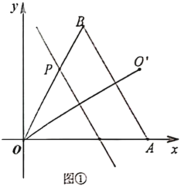
£®2£©»ÁÕº¢⁄£¨µ±µ„![]() ‘⁄
‘⁄![]() ±fl…œ‘À∂Ø ±£¨»Ù÷±œfl
±fl…œ‘À∂Ø ±£¨»Ù÷±œfl![]() £¨«Û
£¨«Û![]() µƒ√ʪ˝£ª
µƒ√ʪ˝£ª
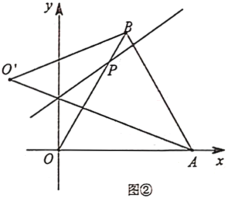
£®3£©µ±![]() ±£¨‘⁄÷±œfl
±£¨‘⁄÷±œfl![]() ±‰ªØπ˝≥Ã÷–£¨«Û
±‰ªØπ˝≥Ã÷–£¨«Û![]() √ʪ˝µƒ◊Ó¥Û÷µ£®÷±Ω”–¥≥ˆΩ·π˚º¥ø…£©£Æ
√ʪ˝µƒ◊Ó¥Û÷µ£®÷±Ω”–¥≥ˆΩ·π˚º¥ø…£©£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
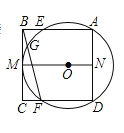
°æƒø°ø»ÁÕº£¨![]() π˝’˝∑Ω–Œ
π˝’˝∑Ω–Œ![]() µƒ∂•µ„
µƒ∂•µ„![]() £¨«“”Î
£¨«“”Î![]() œ‡«–”⁄µ„
œ‡«–”⁄µ„![]() ∑÷±Ωª
∑÷±Ωª![]() ”⁄
”⁄![]() ¡Ωµ„£¨¡¨Ω”
¡Ωµ„£¨¡¨Ω”![]() ≤¢—”≥§Ωª
≤¢—”≥§Ωª![]() ”⁄µ„
”⁄µ„![]() £Æ
£Æ
£®1£©«Û÷§![]()
£®2£©¡¨Ω”![]() Ωª
Ωª![]() ”⁄µ„
”⁄µ„![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨»Ù
£¨»Ù![]() «Û
«Û![]() µƒ≥§£Æ
µƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒfi÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com