
【题目】已知:![]() 内接于
内接于![]() ,
,![]() 为劣弧
为劣弧![]() 的中点,
的中点,![]() .
.
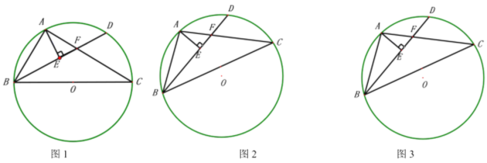
(1)如图1,当![]() 为
为![]() 的直径时,求证:
的直径时,求证:![]() ;
;
(2)如图2,当![]() 不是
不是![]() 的直径,且
的直径,且![]() 时,求证:
时,求证:![]() ;
;
(3)如图3在(2)的条件下,![]() ,
,![]() ,求
,求![]() 长.
长.
【答案】(1)见详解;(2)见详解;(3)![]() .
.
【解析】
(1)由等角的余角相等,得到∠ABD=∠EAC,由![]() 为劣弧
为劣弧![]() 的中点,则∠ABC=2∠EAC,即可得到答案;
的中点,则∠ABC=2∠EAC,即可得到答案;
(2)延长AE交BC于点G,先证明△ABE≌△GBE,则AB=GB,AE=GE,∠BAE=∠BGE,由三角形的外角性质和等量代换,得到CG=AG=2AE,即可得到答案;
(3)延长AE到G,过点D作DH⊥BC,连接DC,OD,由相似三角形的判定和性质,求出所需的边长的长度,结合解直角三角形和勾股定理,即可得到答案.
解:(1)如图1,

∵![]() 为
为![]() 的直径,
的直径,
∴∠BAC=90°,
∵![]() ,
,
∴∠AEF=90°,
∴∠ABD+∠AFB=∠AFB+∠CAE=90°,
∴∠ABD=∠CAE,
∵![]() 为劣弧
为劣弧![]() 的中点,
的中点,
∴∠ABC=2∠ABD=2∠CAE,
∵∠ABC+∠C=90°,
∴![]() ;
;
(2)如图,延长AE交BC于点G,
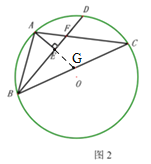
∵AE⊥BD,
∴∠AEB=∠GEB=90°,
∵点D是为劣弧![]() 的中点,
的中点,
∴∠ABE=∠GBE,
∵BE=BE,
∴△ABE≌△GBE(ASA),
∴AB=GB,AE=GE,∠BAE=∠BGE,
∴AG=2AE,
∵![]() ,
,
∴∠BGE=2∠C,
∵∠BGE=∠C+∠CAG,
∴∠C=∠CAG,
∴CG=AG=2AE,
∵BC=BG+CG,
∴![]() ;
;
(3)如图,延长AE到G,过点D作DH⊥BC,连接DC,OD,
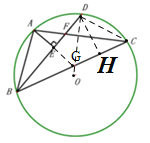
由(2)知,AG=CG,点D为弧AC的中点,
∴点O、G、D三点共线,
∵∠ABE=∠DBH,∠AEB=∠DHB=90°,
∴△ABE∽△DBH,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵DG平分∠AGC,
∴GE=GH,
设![]() ,则
,则![]() ,
,
∴![]() ,
,
在Rt△BEG中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
易证△AFB∽DFC,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,![]() 在平面直角坐标系中,
在平面直角坐标系中,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转,使点
顺时针旋转,使点![]() 落在点
落在点![]() 处,得到
处,得到![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线交
轴的直线交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .
.![]() ,
,![]() .
.
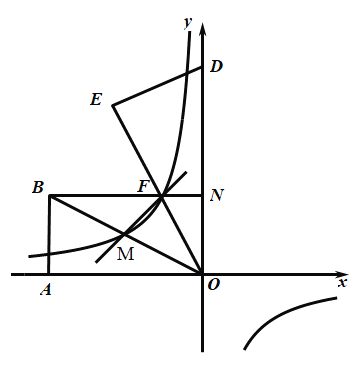
(1)求经过点![]() 、
、![]() 的反比例函数
的反比例函数![]() 和直线
和直线![]() :
:![]() 的解析式;
的解析式;
(2)过点![]() 作
作![]() 轴,求五边形
轴,求五边形![]() 的面积;
的面积;
(3)直接写出当![]() 时
时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
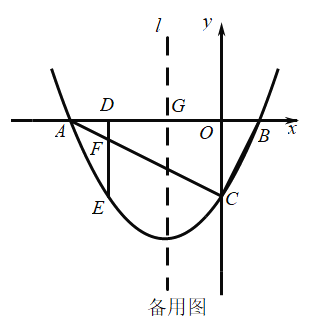
【题目】如图,抛物线![]() 与
与![]() 轴负半轴交于点
轴负半轴交于点![]() ,与
,与![]() 轴正半轴交于点
轴正半轴交于点![]() ,与
,与![]() 轴负半轴交于点
轴负半轴交于点![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求点![]() 的坐标和抛物线的函数关系式;
的坐标和抛物线的函数关系式;
(2)点![]() 是
是![]() 上一点(不与点
上一点(不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线,交抛物线于点
轴的垂线,交抛物线于点![]() ,交
,交![]() 于点
于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)设抛物线的对称轴![]() 交
交![]() 轴于点
轴于点![]() ,在(2)的条件下,点
,在(2)的条件下,点![]() 是抛物线对称轴上一点,点
是抛物线对称轴上一点,点![]() 是坐标平面内一点,是否存在点
是坐标平面内一点,是否存在点![]() 、
、![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,请求出点
为顶点的四边形是菱形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
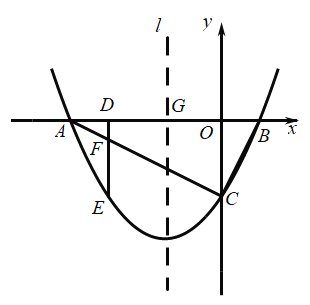
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有![]() 个白球,
个白球,![]() 个黑球和若干个红球,它们除颜色外其余都相同,从中任意摸出
个黑球和若干个红球,它们除颜色外其余都相同,从中任意摸出![]() 个球,是白球的概率为
个球,是白球的概率为![]() .
.
(1)布袋里红球的个数_______;
(2)小亮和小丽将布袋中的白球取出![]() 个,利用剩下的球进行摸球游戏,他们约定:先摸出
个,利用剩下的球进行摸球游戏,他们约定:先摸出![]() 个球后不放回,再摸出
个球后不放回,再摸出![]() 个球,若两个球中有红球则小亮胜,否则小丽胜,你认为这个游戏公平吗?请用列表或画树状图说明理由.
个球,若两个球中有红球则小亮胜,否则小丽胜,你认为这个游戏公平吗?请用列表或画树状图说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小元步行从家去火车站,走到 6 分钟时,以同样的速度回家取物品,然后从家乘出租车赶往火车站,结果比预计步行时间提前了3 分钟.小元离家路程S(米)与时间t(分钟)之间的函数图象如图,从家到火车站路程是( )

A.1300 米B.1400 米C.1600 米D.1500 米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学著作(九章算术)中有如下问题:“今有人持金出五关,前关二而税一.次关三而税一,次关四而税一,次关五而税一,次关六而税一,并五关所税,适重一斤.”其意思为“今有人持金出五关,第![]() 关所收税金为持金的
关所收税金为持金的![]() ,第
,第![]() 关所收税金为剩余金的
关所收税金为剩余金的![]() ,第
,第![]() 关所收税金为剩余金的
关所收税金为剩余金的![]() ,第
,第![]() 关所收税金为剩余金的
关所收税金为剩余金的![]() ,第
,第![]() 关所收税金为剩余金的
关所收税金为剩余金的![]() ,
,![]() 关所收税金之和,恰好重
关所收税金之和,恰好重![]() 斤.”若设这个人原本持金
斤.”若设这个人原本持金![]() 斤,根据题意可列方程为__________ .
斤,根据题意可列方程为__________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的网格中,有两个完全相同的直角三角形纸片,如果把其中一个三角形纸片先横向平移![]() 格,再纵向平移
格,再纵向平移![]() 格,就能使它的一条边与另一个三角形纸片的一条边重合,拼接成一个四边形,那么
格,就能使它的一条边与另一个三角形纸片的一条边重合,拼接成一个四边形,那么![]() 的结果( )
的结果( )

A.只有一个确定的值B.有两个不同的值
C.有三个不同的值D.有三个以上不同的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com