
【题目】如图1,抛物线y=ax2﹣6ax+6(a≠0)与x轴交于点A(8,0),与y轴交于点B,在x轴上有一动点E(m,0)(0<m<8),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
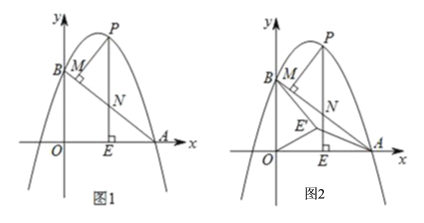
(1)求出抛物线的函数表达式;
(2)设△PMN的面积为S1,△AEN的面积为S2,若S1:S2=36:25,求m的值;
(3)如图2,在(2)条件下,将线段OE绕点O逆时针旋转得到OE′,旋转角为30°,连接E'A、E'B,在坐标平面内找一点Q,使△AOE′~△BOQ,并求出Q的坐标.
【答案】(1)y=-![]() x2+
x2+![]() x+6;(2)m=4;(3)Q1(
x+6;(2)m=4;(3)Q1(![]() ,
,![]() ),Q2(﹣
),Q2(﹣![]() ,
,![]() ).
).
【解析】
(1)把点A(8,0)代入抛物线解析式求解即得;
(2)易求得直线AB解析式为y=![]() x+6,再证明△ANE∽△PNM,由相似三角形的性质得
x+6,再证明△ANE∽△PNM,由相似三角形的性质得![]() ,由E(m,0)(0<m<8)可得P(m,
,由E(m,0)(0<m<8)可得P(m,![]() ),N(m,
),N(m,![]() m+6),然后用m的代数式表示出AN和PN,解方程即可;
m+6),然后用m的代数式表示出AN和PN,解方程即可;
(3)由题意可求得OQ的长,过点Q作QH⊥y轴于H,然后利用∠BOQ=∠AOE′=30°,可求得QH和OH的长,进一步即得结果.
解:(1)把A(8,0)代入y=ax2﹣6ax+6,得64a﹣48a+6=0,解得a=![]() ,
,
∴抛物线的函数表达式为:y=![]() x2+
x2+![]() x+6;
x+6;
(2)如图1,在y=![]() x2+
x2+![]() x+6中,令x=0,得y=6,∴B(0,6),
x+6中,令x=0,得y=6,∴B(0,6),
设直线AB解析式为y=kx+b,则![]() ,解得
,解得 ,
,
∴直线AB解析式为y=![]() x+6
x+6
∵PE⊥x轴,PM⊥AB
∴∠AEN=∠PMN=90°,
∵∠ANE=∠PNM,∴△ANE∽△PNM.
∴![]() ,
,![]() ,
,
∵S1:S2=36:25,

∴![]() ,
,
∴6AN=5PN
∵E(m,0)(0<m<8),∴OE=m,AE=8﹣m,
∴P(m,![]() ),N(m,
),N(m,![]() m+6),
m+6),
∴EN=![]() m+6,PN=PE﹣EN=
m+6,PN=PE﹣EN=![]() ﹣(
﹣(![]() m+6)=
m+6)=![]() +3m,
+3m,
∵AB=![]() =10
=10
∴cos∠OAB=![]() ,即
,即![]() ,
,
∴AN=![]() (8﹣m),
(8﹣m),
∴6×![]() (8﹣m)=5×(
(8﹣m)=5×(![]() +3m),解得:m1=4,m2=8(不符合题意,舍去),
+3m),解得:m1=4,m2=8(不符合题意,舍去),
∴m=4;
(3)如图2,∵线段OE绕点O逆时针旋转得到OE′,旋转角为30°,
∴OE′=OE=4,∠AOE′=30°
∵△AOE′∽△BOQ,
∴![]() ,∠BOQ=∠AOE′=30°,
,∠BOQ=∠AOE′=30°,
∴![]() ,即OQ=3,
,即OQ=3,
过点Q作QH⊥y轴于H,
∴QH=![]() OQ=
OQ=![]() ,OH=
,OH=![]() ,
,
∴当点Q在y轴右侧时,Q1(![]() ,
,![]() ),
),
当点Q在y轴左侧时,Q2(﹣![]() ,
,![]() ).
).
综上所述,Q的坐标为:Q1(![]() ,
,![]() ),Q2(﹣
),Q2(﹣![]() ,
,![]() ).
).



 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
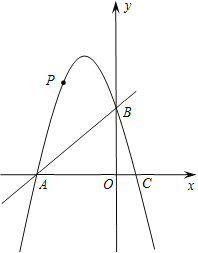
【题目】如图,在平面直角坐标系中,直线y=x+4与x轴、y轴分别交于A、B两点,抛物线y=-x2+bx+c经过A、B两点,并与x轴交于另一点C(点C点A的右侧),点P是抛物线上一动点.
(1)求抛物线的解析式及点C的坐标;
(2)若点P在第二象限内,过点P作PD⊥轴于D,交AB于点E.当点P运动到什么位置时,线段PE最长?此时PE等于多少?
(3)如果平行于x轴的动直线l与抛物线交于点Q,与直线AB交于点N,点M为OA的中点,那么是否存在这样的直线l,使得△MON是等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
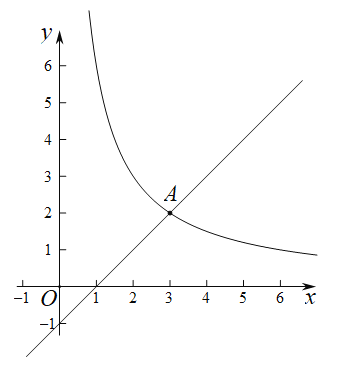
【题目】如图,已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,点
,点![]() .
.
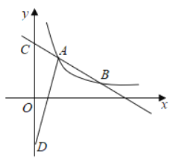
(1)求反比例函数的表达式;
(2)若一次函数图象与![]() 轴交于点C,点D为点C关于原点O的对称点,求
轴交于点C,点D为点C关于原点O的对称点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段铁路的示意图,![]() 段和
段和![]() 段都是高架桥,
段都是高架桥,![]() 段是隧道.已知
段是隧道.已知![]() ,
,![]() ,
,![]() ,在
,在![]() 段高架桥上有一盏吊灯,当火车驶过时,灯光可垂直照射到车身上,已知火车甲沿
段高架桥上有一盏吊灯,当火车驶过时,灯光可垂直照射到车身上,已知火车甲沿![]() 方向匀速行驶,当火车甲经过吊灯时,灯光照射到火车甲上的时间是
方向匀速行驶,当火车甲经过吊灯时,灯光照射到火车甲上的时间是![]() ,火车甲通过隧道的时间是
,火车甲通过隧道的时间是![]() ,如果从车尾经过点
,如果从车尾经过点![]() 时开始计时,设行驶的时间为
时开始计时,设行驶的时间为![]() ,车头与点
,车头与点![]() 的距离是
的距离是![]() .
.

(1)火车甲的速度和火车甲的长度
(2)求![]() 关于
关于![]() 的函数解析式(写出
的函数解析式(写出![]() 的取值范围),并求当
的取值范围),并求当![]() 为何值时,车头差
为何值时,车头差![]() 米到达
米到达![]() 点.
点.
(3)若长度相等的火车乙以相同的速度沿![]() 方向行驶,且火车甲乙不在隧道内会车(会车时两车均不在隧道内),火车甲先进隧道,当火车甲的车头到达
方向行驶,且火车甲乙不在隧道内会车(会车时两车均不在隧道内),火车甲先进隧道,当火车甲的车头到达![]() 点时,火车乙的车头能否到达
点时,火车乙的车头能否到达![]() 点?若能到达,至多驶过地点多少?若不能到达,至少距离
点?若能到达,至多驶过地点多少?若不能到达,至少距离![]() 点多少
点多少![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠BAD=![]() ,E为对角线AC上的一点(不与A,C重合),将射线EB绕点E顺时针旋转
,E为对角线AC上的一点(不与A,C重合),将射线EB绕点E顺时针旋转![]() 角之后,所得射线与直线AD交于F点.试探究线段EB与EF的数量关系.
角之后,所得射线与直线AD交于F点.试探究线段EB与EF的数量关系.
小宇发现点E的位置,![]() 和
和![]() 的大小都不确定,于是他从特殊情况开始进行探究.
的大小都不确定,于是他从特殊情况开始进行探究.
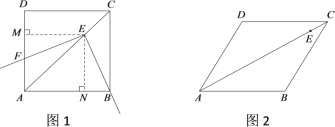
(1)如图1,当![]() =
=![]() =90°时,菱形ABCD是正方形.小宇发现,在正方形中,AC平分∠BAD,作EM⊥AD于M,EN⊥AB于N.由角平分线的性质可知EM=EN,进而可得
=90°时,菱形ABCD是正方形.小宇发现,在正方形中,AC平分∠BAD,作EM⊥AD于M,EN⊥AB于N.由角平分线的性质可知EM=EN,进而可得![]() ,并由全等三角形的性质得到EB与EF的数量关系为 .
,并由全等三角形的性质得到EB与EF的数量关系为 .
(2)如图2,当![]() =60°,
=60°,![]() =120°时,
=120°时,
①依题意补全图形;
②请帮小宇继续探究(1)的结论是否成立.若成立,请给出证明;若不成立,请举出反例说明;
(3)小宇在利用特殊图形得到了一些结论之后,在此基础上对一般的图形进行了探究,设∠ABE=![]() ,若旋转后所得的线段EF与EB的数量关系满足(1)中的结论,请直接写出角
,若旋转后所得的线段EF与EB的数量关系满足(1)中的结论,请直接写出角![]() ,
,![]() ,
,![]() 满足的关系: .
满足的关系: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,反比例函数
中,反比例函数![]() 的图象与直线
的图象与直线![]() 交于点
交于点![]()
(1)求k的值;
(2)已知点![]() ,过点P作垂直于x轴的直线,交直线
,过点P作垂直于x轴的直线,交直线![]() 于点B,交函数
于点B,交函数![]() 于点C.
于点C.
①当![]() 时,判断线段
时,判断线段![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
②若![]() ,结合图象,直接写出n的取值范围.
,结合图象,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
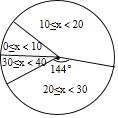
【题目】体育组为了了解九年级450名学生排球垫球的情况,随机抽查了九年级部分学生进行排球垫球测试(单位:个),根据测试结果,制成了下面不完整的统计图表:
组别 | 个数段 | 频数 | 频率 |
1 |
| 5 | 0.1 |
2 |
| 21 | 0.42 |
3 |
|
| |
4 |
|
|
(1)表中的数![]() ,
,![]() ;
;
(2)估算该九年级排球垫球测试结果小于10的人数;
(3)排球垫球测试结果小于10的为不达标,若不达标的5人中有3个男生,2个女生,现从这5人中随机选出2人调查,试通过画树状图或列表的方法求选出的2人为一个男生一个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习“三角形的内角和外角”时,老师在学案上设计了以下内容:
如图,已知△ABC,对∠A+∠B+∠ACB=180°的说理过程如下:
延长BC到点D,过点C作CE∥AB.
∵CE∥AB.
∴∠A=①(两直线平行,内错角相等).
∠B=②(两直线平行,同位角相等).
∵∠ACB+③+④=180°(平角定义).
∴∠A+∠B+∠ACB=180°(等量代换).
下列选项正确的是( )
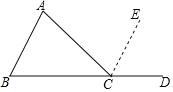
A.①处填∠ECDB.②处填∠ECDC.③处填∠AD.④处填∠B
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com