
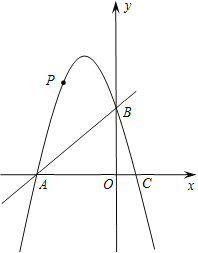
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=x��4��x�ᡢy��ֱ���A��B���㣬������y=��x2��bx��c����A��B���㣬����x�ύ����һ��C����C��A���Ҳࣩ����P����������һ���㣮
��1���������ߵĽ���ʽ����C�����ꣻ
��2������P�ڵڶ������ڣ�����P��PD������D����AB�ڵ�E������P�˶���ʲôλ��ʱ���߶�PE�����ʱPE���ڶ��٣�
��3�����ƽ����x��Ķ�ֱ��l�������߽��ڵ�Q����ֱ��AB���ڵ�N����MΪOA���е㣬��ô�Ƿ����������ֱ��l��ʹ����MON�ǵ��������Σ������ڣ��������Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y=��x2��3x��4��C��1��0����2����t=-2ʱ���߶�PE�ij��������ֵ4����ʱP����2��6����3������������ֱ��l��ʹ����MONΪ���������Σ�����Q�������Ϊ
��![]() ��3����
��3����![]() ��3����
��3����![]() ��2����
��2����![]() ��2��
��2��
��������
�⣺��1����ֱ��y=x+4��x�ᡢy��ֱ���A��B���㣬��A����4��0����B��0��4����
��������y=��x2��bx��c����A��B���㣬
��![]() �����
�����![]() ��
��
�������߽���ʽΪy=��x2��3x��4��
��y=0���ã�x2��3x��4=0�����x1=��4��x2=1��
��C��1��0����
��2����ͼ1��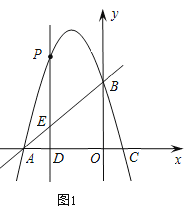
��D��t��0����
��OA=OB�����BAO=45����
��E��t��t��4����P��t����t2��3t��4����
PE=yP��yE=��t2��3t��4��t��4=��t2��4t=����t+2��2+4��
����t=-2ʱ���߶�PE�ij��������ֵ4����ʱP����2��6����
��3�����ڣ���ͼ2����N����NH��x���ڵ�H��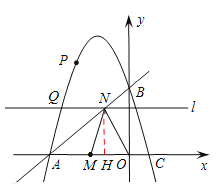
��OH=m��m��0������OA=OB�����BAO=45����
��NH=AH=4��m����yQ=4��m��
��MΪOA�е㣬��MH=2��m��
����MONΪ����������ʱ��
����MN=ON����HΪ�ױ�OM���е㣬
��m=1����yQ=4��m=3��
�ɣ�xQ2��3xQ��4=3�����![]() ��
��
����Q������![]() ��3����
��3����![]() ��3����
��3����
����MN=OM=2������Rt��MNH��
���ݹ��ɶ����ã�MN2=NH2��MH2����22=��4��m��2����2��m��2��
�����m2��6m��8=0����ã�m1=2��m2=4���������⣬��ȥ����
��yQ=2���ɣ�xQ2��3xQ��4=2�����![]() ��
��
����Q������![]() ��2����
��2����![]() ��2����
��2����
����ON=OM=2������Rt��NOH��
���ݹ��ɶ����ã�ON2=NH2��OH2����22=��4��m��2��m2��
�����m2��4m��6=0���ߡ�=��8��0��
����ʱ������������ֱ��l��ʹ����MONΪ���������Σ�
��������������������ֱ��l��ʹ����MONΪ���������Σ�����Q�������Ϊ
��![]() ��3����
��3����![]() ��3����
��3����![]() ��2����
��2����![]() ��2����
��2����
��1���������A��B������꣬Ȼ�����ô���ϵ�����������ߵĽ���ʽ���������������x����һ����C�����꣮
��2������߶�PE���ȵı���ʽ����D�������Ϊt������Խ�PE��ʾΪ����t�Ķ��κ��������ö��κ�����ֵ�ķ������PE���ȵ����ֵ��
��3�����ݵ��������ε����ʺ��ɶ�������ֱ��l�Ĵ���������ת��ΪһԪ���η������⣬ͨ��һԪ���η��̵��б�ʽ��ֱ֪��l�Ƿ���ڣ��������ӦQ������꣮ ����MON�ǵ����������������а������������MN=ON��MN=OM��ON=OM����һ������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
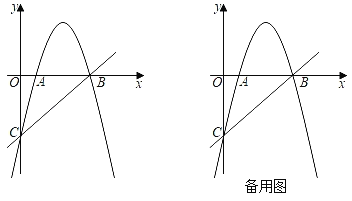
����Ŀ����ͼ��������y��ax2+6x+c��x����A��B���㣬��y���ڵ�C��ֱ��y��x��5������B��C��
��1���������ߵĽ���ʽ��
��2������NΪ�������϶��㣬����NBA����OACʱ�����N�����꣬
��3������A��ֱ�߽�ֱ��BC�ڵ�M����AM��BCʱ������������һ����P�������B��C�غϣ�����ֱ��AM��ƽ���߽�ֱ��BC�ڵ�Q�����Ե�A��M��Q��PΪ������ı�����ƽ���ı��Σ����P�ĺ����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
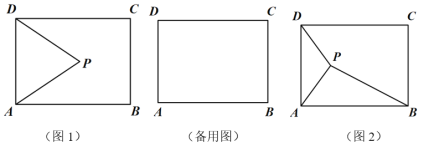
����Ŀ�����Ķ����⣩���P�ھ���ABCD�ڲ�������P�����ε�һ���ߵ������˵�������ʱ���Ƶ�PΪ�ñߵ�����г���������磺��ͼ1������ABCD�У���PA��PD�����PΪ��AD������г������
���������ã���֪����P�ھ���ABCD�ڲ�����AB=10��BC=6��
��1����P�DZ�AD�������������P ��BC���������������������������������
��2����P�DZ�BC������г����������PA��PB������PAB��ֱ��������ʱ����PA��ֵ��
��3����ͼ2����P�DZ�AD������г����������PA��PB��PD����tan��PAB�� tan��PBA����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ϣ�������ıϴ����˹ѧ�ɰ�1��3��6��10����������������Ϊ������������������1��4��16����������������Ϊ����������������ͼ�п��Է��֣��κ�һ������1�ġ����������������Կ����������ڡ�����������֮�ͣ�������ͼʾ�еĹ��ɣ���д����9����ʽ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������Ϊ8cm����4cm�ľ���ֽƬABCD�۵���ʹ��A��C�غϣ����ۺ�EF�ij�Ϊ��������
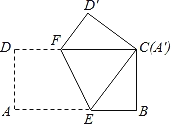
A.8cmB.4![]() cmC.5cmD.2
cmC.5cmD.2![]() cm
cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���![]() �У�
��![]() ��
��![]() ��
��
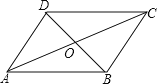
��1����֤���ı���![]() Ϊƽ���ı��Σ�
Ϊƽ���ı��Σ�
��2����![]() ��
��![]() �����ı���
�����ı���![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˸��õ����ҵ�������������ʶ��ijС����ҵ����ίԱ�������С���ڰ�װ�����������ܰ��ʾ�ƺ������䣬������3����ܰ��ʾ�ƺ�2�������乲��Ҫ420Ԫ����ÿ����ܰ��ʾ�Ʊ����������60Ԫ��
��1���ʹ���1����ܰ��ʾ�ƺ�1�����������Ҫ����Ԫ��
��2�������Ҫ������ܰ��ʾ�ƺ������乲80�����ҷ��ò�����8000Ԫ���������Թ�����������ٸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�У�ֱ��y=��![]() x�뷴��������y=
x�뷴��������y=![]() ��ͼ���ڹ���ԭ��ԳƵ�A��B���㣬��֪A�����������3��
��ͼ���ڹ���ԭ��ԳƵ�A��B���㣬��֪A�����������3��
��1�����������ı���ʽ��
��2����ֱ��y=��![]() x����ƽ�ƺ��뷴���������ڵڶ������ڽ��ڵ�C�������ABC�����Ϊ48����ƽ�ƺ��ֱ�ߵĺ�������ʽ��
x����ƽ�ƺ��뷴���������ڵڶ������ڽ��ڵ�C�������ABC�����Ϊ48����ƽ�ƺ��ֱ�ߵĺ�������ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������y��ax2��6ax+6��a��0����x�ύ�ڵ�A��8��0������y�ύ�ڵ�B����x������һ����E��m��0����0��m��8��������E��x��Ĵ��߽�ֱ��AB�ڵ�N�����������ڵ�P������P��PM��AB�ڵ�M��
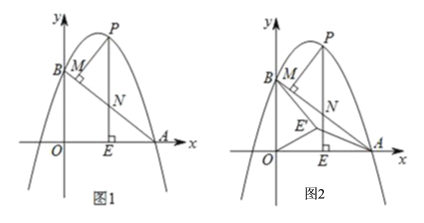
��1����������ߵĺ�������ʽ��
��2������PMN�����ΪS1����AEN�����ΪS2����S1��S2��36��25����m��ֵ��
��3����ͼ2���ڣ�2�������£����߶�OE�Ƶ�O��ʱ����ת�õ�OE������ת��Ϊ30��������E'A��E'B��������ƽ������һ��Q��ʹ��AOE������BOQ�������Q�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com