练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知一次函数的图象与反比例函数的图象交于点，点．

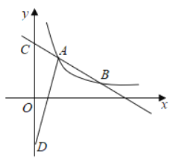
    （1）求反比例函数的表达式；

    （2）若一次函数图象与轴交于点C，点D为点C关于原点O的对称点，求的面积．

    【答案】（1）；（2）18

    【解析】

    （1）根据点A、B都在反比例函数图象上，得到关于a的方程，求出a，即可求出反比例函数解析式；

    （2）根据点A、B都在一次函数的图象上，运用待定系数法求出直线解析式，进而求出点C坐标，求出CD长，即可求出的面积．

    解：（1）∵点，点在反比例函数的图象上，

    ∴．

    解得．

    ∴．

    ∴反比例函数的表达式是．

    （2）∵，

    ∴点A，点B的坐标分别是．

    ∵点A，点B在一次函数的图象上，

    ∴

    解得

    ∴一次函数的表达式是．

    当时，．

    ∴点C的坐标是．

    ∴．

    ∵点D是点C关于原点O的对称点，

    ∴．

    作轴于点E，

    ∴．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

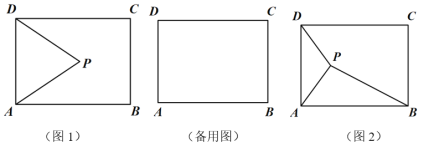
    【题目】（阅读理解）设点P在矩形ABCD内部，当点P到矩形的一条边的两个端点距离相等时，称点P为该边的“和谐点”．例如：如图1，矩形ABCD中，若PA＝PD，则称P为边AD的“和谐点”．

    （解题运用）已知，点P在矩形ABCD内部，且AB=10，BC=6．

    （1）设P是边AD的“和谐点”，则P 边BC的“和谐点”（填“是”或“不是”）；

    （2）若P是边BC的“和谐点”，连接PA，PB，当△PAB是直角三角形时，求PA的值；

    （3）如图2，若P是边AD的“和谐点”，连接PA，PB，PD，求tan∠PAB· tan∠PBA的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了更好地提高业主垃圾分类的意识，某小区物业管理委员会决定在小区内安装垃圾分类的温馨提示牌和垃圾箱，若购买3个温馨提示牌和2个垃圾箱共需要420元，且每个温馨提示牌比垃圾箱便宜60元．

    （1）问购买1个温馨提示牌和1个垃圾箱各需要多少元？

    （2）如果需要购买温馨提示牌和垃圾箱共80个，且费用不超过8000元，问最多可以购买垃圾箱多少个？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在直角坐标系中，直线y=﹣x与反比例函数y=的图象交于关于原点对称的A，B两点，已知A点的纵坐标是3．

    （1）求反比例函数的表达式；

    （2）将直线y=﹣x向上平移后与反比例函数在第二象限内交于点C，如果△ABC的面积为48，求平移后的直线的函数表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在信息快速发展的社会，“信息消费”已成为人们生活的重要组成部分，某高校组织课外小组在我市的一个社区随机抽取部分家庭，调查每月用于信息消费的金额，根据数据整理成如下不完整统计表和统计图（如图）．已知，两组户数频数宜方图的高度比为1：5．

    月信息消费额分组统计表

    组别

    消费额/元

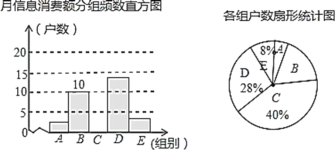
    请结合图表中相关数据解答下列问题：

    （1）这次接受调查的有_________户；

    （2请你补全频数直方图；

    （3）以各组组中值代表本组的月信息消费额的平均数，计算课外小组抽取家庭的月信息消费额的平均数；

    （4）若该社区有2000户住户，请估计月信息消费额不少于200元的户数是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若一次函数的图象与轴，轴分别交于A，C两点，点B的坐标为，二次函数的图象过A，B，C三点，如图（1）．

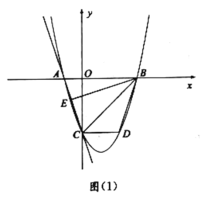
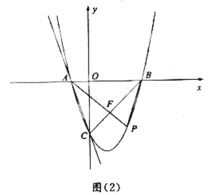
    （1）求二次函数的表达式；

    （2）如图（1），过点C作轴交抛物线于点D，点E在抛物线上（轴左侧），若恰好平分．求直线的表达式；

    （3）如图（2），若点P在抛物线上（点P在轴右侧），连接交于点F，连接，．

    ①当时，求点P的坐标；

    ②求的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，菱形中，对角线、相交于点，，，动点从点出发，沿线段以的速度向点运动，同时动点从点出发，沿线段以支向点运动，当其中一个动点停止时另一个动点也随之停止，设运动时间为（单位：）（），以点为圆心，长为半径的⊙M与射线、线段分别交于点、，连接．

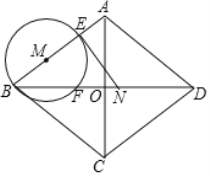
    （1）求的长（用含有的代数式表示），并求出的取值范围；

    （2）当为何值时，线段与⊙M相切？

    （3）若⊙M与线段只有一个公共点，求的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，抛物线y＝ax2﹣6ax+6（a≠0）与x轴交于点A（8，0），与y轴交于点B，在x轴上有一动点E（m，0）（0＜m＜8），过点E作x轴的垂线交直线AB于点N，交抛物线于点P，过点P作PM⊥AB于点M．

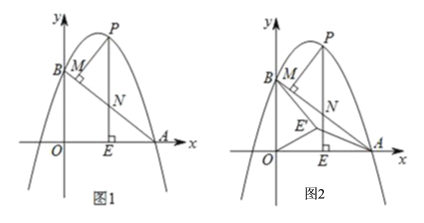
    （1）求出抛物线的函数表达式；

    （2）设△PMN的面积为S1，△AEN的面积为S2，若S1：S2＝36：25，求m的值；

    （3）如图2，在（2）条件下，将线段OE绕点O逆时针旋转得到OE′，旋转角为30°，连接E'A、E'B，在坐标平面内找一点Q，使△AOE′～△BOQ，并求出Q的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

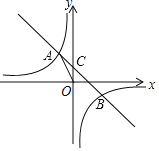
    【题目】如图，在平面直角坐标系中，一次函数y＝ax+b的图象与反比例函数y＝﹣的图象交于二、四象限内的A、B两点，与y轴交于C点，点A的坐标为（m，3），点B与点A关于直线y＝x对称．

    （1）求直线AB的解析式；

    （2）P是y轴上一点，且S△PBC＝2S△AOB，求点P的坐标．

    查看答案和解析>>

    同步练习册答案