
【题目】在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分,某高校组织课外小组在我市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如下不完整统计表和统计图(如图).已知![]() ,
,![]() 两组户数频数宜方图的高度比为1:5.
两组户数频数宜方图的高度比为1:5.
月信息消费额分组统计表
组别 | 消费额/元 |
|
|
|
|
|
|
|
|
|
|
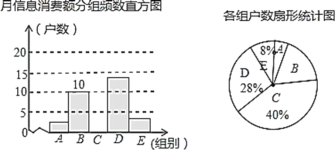
请结合图表中相关数据解答下列问题:
(1)这次接受调查的有_________户;
(2请你补全频数直方图;
(3)以各组组中值代表本组的月信息消费额的平均数,计算课外小组抽取家庭的月信息消费额的平均数;
(4)若该社区有2000户住户,请估计月信息消费额不少于200元的户数是多少?
【答案】(1)50;(2)答案见解析;(3)266;(4)1520.
【解析】
(1)根据A、B两组户数直方图的高度比为1:5,即两组的频数的比是1:5,据此即可求得A组的频数;利用A和B两组的频数的和除以两组所占的百分比即可求得总数,即样本容量
(2)利用总数乘以百分比即可求得C组的频数,从而补全统计图;
(3)求出各组的频数,利用频数乘以组中值,根据平均数计算公式求出平均数;
(4)利用总数2000乘以月信息消费额不少于200的百分比之和即可.
解:(1)![]() A,B两组户数频数直方图的高度比为
A,B两组户数频数直方图的高度比为![]()
∴A组的频数为2
这次接受调查的户数为![]()
(2)C组的频数是:![]() ,如图;
,如图;
(3)![]()
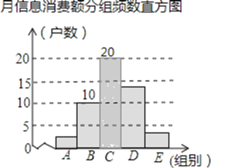
(4)![]() (户),
(户),
答:估计月信息消费额不少于200元的约有1520户.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
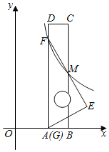
【题目】如图,将一把矩形直尺ABCD和一块含30°角的三角板EFG摆放在平面直角坐标系中,AB在x轴上,点G与点A重合,点F在AD上,三角板的直角边EF交BC于点M,反比例函数![]() (x
(x![]() 0)的图象恰好经过点F,M.若直尺的宽CD=2,三角板的斜边FG=
0)的图象恰好经过点F,M.若直尺的宽CD=2,三角板的斜边FG=![]() ,则k=____.
,则k=____.
查看答案和解析>>
科目:初中数学 来源: 题型:
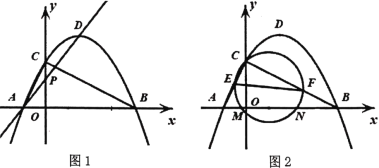
【题目】如图![]() ,二次函数
,二次函数![]() (
(![]() 、
、![]() 为参数,其中
为参数,其中![]() )的图象与
)的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() .
.
(1)若![]() ,求
,求![]() 的值(结果用含
的值(结果用含![]() 的式子表示);
的式子表示);
(2)若![]() 是等腰三角形,直线
是等腰三角形,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,且
,且![]() .求抛物线的解析式;
.求抛物线的解析式;
(3)如图![]() ,已知
,已知![]() ,
,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 上的动点,且
上的动点,且![]() ,若以
,若以![]() 为直径的圆经过点
为直径的圆经过点![]() ,并交
,并交![]() 轴于
轴于![]() 、
、![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
折纸是同学们喜欢的手工活动之一,通过折纸我们既可以得到许多美丽的图形,同时折纸的过程还蕴含着丰富的数学知识.折一折:把边长为![]() 的正方形纸片
的正方形纸片![]() 对折,使边
对折,使边![]() 与
与![]() 重合,展开后得到折痕
重合,展开后得到折痕![]() .如图①:点
.如图①:点![]() 为
为![]() 上一点,将正方形纸片
上一点,将正方形纸片![]() 沿直线
沿直线![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 上的点
上的点![]() 处,展开后连接
处,展开后连接![]() ,
,![]() ,
,![]() ,如图②
,如图②
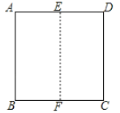
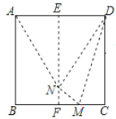
图① 图②
(一)填一填,做一做:
(1)图②中,![]() _______.线段
_______.线段![]() _______.
_______.
(2)图②中,试判断![]() 的形状,并给出证明.
的形状,并给出证明.
剪一剪、折一折:将图②中的![]() 剪下来,将其沿直线
剪下来,将其沿直线![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处,分别得到图③、图④.
处,分别得到图③、图④.
(二)填一填
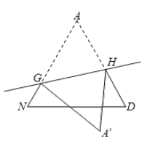
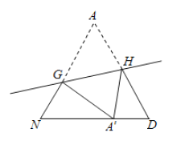
图③ 图④
(3)图③中阴影部分的周长为_______.
(4)图③中,若![]() ,则
,则![]() _______°.
_______°.
(5)图③中的相似三角形(包括全等三角形)共有_______对;
(6)如图④点![]() 落在边
落在边![]() 上,若
上,若![]() _______,则
_______,则![]() _______用含
_______用含![]() ,
,![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠CBG=∠A,CD为直径,OC与AB相交于点E,过点E作EF⊥BC,垂足为F,延长CD交GB的延长线于点P,连接BD.
(1)求证:PG与⊙O相切;
(2)若![]() =
=![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,若⊙O的半径为8,PD=OD,求OE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,点
,点![]() .
.
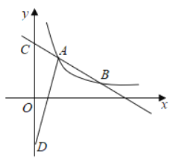
(1)求反比例函数的表达式;
(2)若一次函数图象与![]() 轴交于点C,点D为点C关于原点O的对称点,求
轴交于点C,点D为点C关于原点O的对称点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解该校八年级全体学生一周内平均每天参加课外锻炼的时间,从中随机抽查了部分学生,并将抽查结果绘制成如下图表:
分组 | 频数 | 频率 |
9.5~19.5 | 2 | 0.05 |
19.5~29.5 | 4 | 0.1 |
29.5~39.5 | 10 |
|
39.5~49.5 |
| 0.35 |
49.5~59.5 | 7 | 0.175 |
59.5~69.5 | 3 | 0.075 |
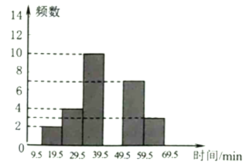
(1)表中![]() 、
、![]() 表示的数分别为:
表示的数分别为:![]() ________,
________,![]() _________;
_________;
(2)请补全频数直方图;
(3)如果该校八年级有800名学生,估计一下平均每天参加课外锻炼达![]() 以上的学生有多少人?
以上的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠BAD=![]() ,E为对角线AC上的一点(不与A,C重合),将射线EB绕点E顺时针旋转
,E为对角线AC上的一点(不与A,C重合),将射线EB绕点E顺时针旋转![]() 角之后,所得射线与直线AD交于F点.试探究线段EB与EF的数量关系.
角之后,所得射线与直线AD交于F点.试探究线段EB与EF的数量关系.
小宇发现点E的位置,![]() 和
和![]() 的大小都不确定,于是他从特殊情况开始进行探究.
的大小都不确定,于是他从特殊情况开始进行探究.
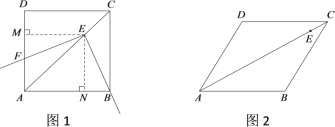
(1)如图1,当![]() =
=![]() =90°时,菱形ABCD是正方形.小宇发现,在正方形中,AC平分∠BAD,作EM⊥AD于M,EN⊥AB于N.由角平分线的性质可知EM=EN,进而可得
=90°时,菱形ABCD是正方形.小宇发现,在正方形中,AC平分∠BAD,作EM⊥AD于M,EN⊥AB于N.由角平分线的性质可知EM=EN,进而可得![]() ,并由全等三角形的性质得到EB与EF的数量关系为 .
,并由全等三角形的性质得到EB与EF的数量关系为 .
(2)如图2,当![]() =60°,
=60°,![]() =120°时,
=120°时,
①依题意补全图形;
②请帮小宇继续探究(1)的结论是否成立.若成立,请给出证明;若不成立,请举出反例说明;
(3)小宇在利用特殊图形得到了一些结论之后,在此基础上对一般的图形进行了探究,设∠ABE=![]() ,若旋转后所得的线段EF与EB的数量关系满足(1)中的结论,请直接写出角
,若旋转后所得的线段EF与EB的数量关系满足(1)中的结论,请直接写出角![]() ,
,![]() ,
,![]() 满足的关系: .
满足的关系: .
查看答案和解析>>
科目:初中数学 来源: 题型:
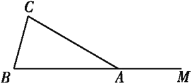
【题目】如图,在△ABC中,AB=AC,点M在BA的延长线上.
(1)按下列要求作图,并在图中标明相应的字母.(保留作图痕迹)
①作∠MAC的平分线AN;
②作AC的中点O,连结BO,并延长BO交AN于点D,连结CD;
(2)在(1)的条件下,判断四边形ABCD的形状,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com