【题目】如图，在长方形 ABCD 中，AB＝5，AD＝13，点 E 为 BC 上一点，将△ABE沿 AE 折叠，使点 B 落在长方形内点 F 处，连接 DF 且 DF＝12．
（1）试说明：△ADF 是直角三角形；
（2）求 BE 的长．
【答案】（1）见解析；（2）1．
【解析】
（1）由折叠的性质可知AF=AB=5，然后再依据勾股定理的逆定理可证明△ADF为直角三角形；
（2）由题意可证点E、D、F在一条直线上，设BE=x，则EF=x，DE=12+x，EC=13-x，在Rt△CED中，依据勾股定理列方程求解即可．
解：（1）将△ABE沿AE折叠，使点B落在长方形内点F处，
∴AF=AB=5，
∵
=25+144=169=
=
，
∴∠AFD=90°
∴△ADF是直角三角形；
（2）∵折叠
∴BE=EF，∠B=∠AFE=90°
又∵∠AFD=90°
∴点D，F，E在一条直线上．
设BE=x，则EF=x，DE=12+x，EC=13-x，
在Rt△CED中，∠C=90°，
∴
，
即
．
∴x=1．
∴BE=1．
科目：初中数学 来源： 题型：
【题目】列方程解应用题：某商场经市场调查，预计一款夏季童装能获得市场青睐，便花费15000元购进了一批此款童装，上市后很快售罄．该店决定继续进货，由于第二批进货数量是第一批进货数量的2倍，因此单价便宜了10元，购进第二批童装一共花费了27000元．那该店所购进的第一批童装的价格是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了解某地区七年级学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，从该地区随机抽取部分七年级学生作为样本，采用问卷调查的方法收集数据（参与问卷调查的每名同学只能选择其中一类节目），并调查得到的数据用下面的表和扇形图来表示（表、图都没制作完成）
根据表、图提供的信息，解决以下问题：
（1）计算出表中a、b的值；
（2）求扇形统计图中表示“动画”部分所对应的扇形的圆心角度数；
（3）若该地区七年级学生共有47500人，试估计该地区七年级学生中喜爱“新闻”类电视节目的学生有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（本题6分）如图，已知△ABC，∠C=Rt∠，AC<BC，D为BC上一点，且到A，B两点的距离相等．
（1）用直尺和圆规，作出点D的位置（不写作法，保留作图痕迹）；
（2）连结AD，若∠B=37°，求∠CAD的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在边长为
的菱形
中，对角线
，点
是直线
上的动点，
于
，
于
．
如图，在边长为的菱形中，对角线，点是直线上的动点，于，于．
对角线
的长是________，菱形的面积是________；
如图
，当点在对角线上运动时，
的值是否发生变化？请说明理由；
如图
，当点在对角线的延长线上时，的值是否发生变化？若不变请说明理由，若变化，请直接写出
、
之间的数量关系，不用明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，BE⊥CD 垂足为 E，BE＝DE=8，BC＝DA
求证：（1）△BEC≌△DEA；
（2）若 MN 是边 AD 的垂直平分线，分别交 AD、CD 于 M、N，且 CE=5,求△AEN 的周长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，∠AOB=120°，OP平分∠AOB，且OP=2，若点M，N分别在OA，OB上，且△PMN为等边三角形，则满足上述条件的△PMN有（ ）
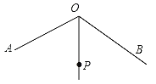
A.2个B.3个C.4个D.无数个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为测量一河两岸相对电线杆
、
之间的距离，有四位同学分别测量出了一下四组数据：
①
，
；②
，，
；③
，
，
；④，
，；
能根据所测数据，求出、间距离的共有（ ）
A. 1组 B. 2组 C. 3组 D. 4组
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，长方形纸片ABCD（长方形的对边平行且相等，每个角都为直角），将纸片沿EF折叠，使点C与点A重合，下列结论：①AF＝AE，②△ABE≌△AGF，③AF＝CE，④∠AEF＝60°，正确的有_____．（填写序号）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com