
【题目】为了解某地区七年级学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,从该地区随机抽取部分七年级学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名同学只能选择其中一类节目),并调查得到的数据用下面的表和扇形图来表示(表、图都没制作完成)
 根据表、图提供的信息,解决以下问题:
根据表、图提供的信息,解决以下问题:
(1)计算出表中a、b的值;
(2)求扇形统计图中表示“动画”部分所对应的扇形的圆心角度数;

(3)若该地区七年级学生共有47500人,试估计该地区七年级学生中喜爱“新闻”类电视节目的学生有多少人?
【答案】(1)162,135;(2)108°;(3)3800.
【解析】
(1)先求出抽取的总人数,再求出b的值,进而可得出a的值;
(2)求出a的值与总人数的比可得出结论;
(3)求出喜爱新闻类人数的百分比,进而可得出结论.
(1)∵喜欢体育的人数是90人,占总人数的20%,∴总人数=![]() =450(人).
=450(人).
∵娱乐人数占36%,∴a=450×36%=162(人),∴b=450﹣162﹣36﹣90﹣27=135(人);
(2)∵喜欢动画的人数是135人,∴![]() ×360°=108°;
×360°=108°;
(3)∵喜爱新闻类人数的百分比=![]() ×100%=8%,∴47500×8%=3800(人).
×100%=8%,∴47500×8%=3800(人).
答:该地区七年级学生中喜爱“新闻”类电视节目的学生有3800人.


科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=BC=4,把△ABC沿AC翻折得到△ADC.则
(1)四边形ABCD是 形;
(2)若∠B=120°,点P、E、F分别为线段AC、AD、DC上的任意1点,则PE+PF的最小值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列的解答过程,然后再解答:
形如![]() 的化简,只要我们找到两个正数a、b,使a+b=m,ab=n,使得
的化简,只要我们找到两个正数a、b,使a+b=m,ab=n,使得![]() ,
,![]() ,那么便有:
,那么便有:![]() (a>b)
(a>b)
例如:化简![]()
解:首先把![]() 化为
化为![]() ,这里m=7,n=12,由于4+3=7,4×3=12
,这里m=7,n=12,由于4+3=7,4×3=12
即![]() ,
,![]()
∴![]() =
=![]()
(1)填空:![]() = ,
= ,![]() = ;
= ;
(2)化简:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小马、小虎两人共同计算一道题:(x+a)(2x+b).由于小马抄错了a的符号,得到的结果是2x2﹣7x+3,小虎漏抄了第二个多项式中x的系数得到的结果是x2+2x﹣3.
(1)求a,b的值;
(2)细心的你请计算这道题的正确结果;
(3)当x=﹣1时,计算(2)中的代数式的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三条边都相等的三角形叫做等边三角形,它的三个角都是60°.△ABC是等边三角形,点D在BC所在直线上运动,连接AD,在AD所在直线的右侧作∠DAE=60°,交△ABC的外角∠ACF的角平分线所在直线于点E.
(1)如图1,当点D在线段BC上时,请你猜想AD与AE的大小关系,并给出证明;
(2)如图2,当点D在线段BC的反向延长线上时,依据题意补全图形,请问上述结论还成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则点A2 019的坐标为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,且AD=2,AC=BC=![]() .
.
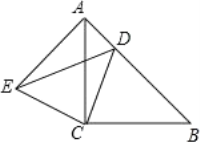
(1)证明:△ACE≌△BCD;
(2)求四边形ADCE的面积;
(3)求ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形 ABCD 中,AB=5,AD=13,点 E 为 BC 上一点,将△ABE沿 AE 折叠,使点 B 落在长方形内点 F 处,连接 DF 且 DF=12.

(1)试说明:△ADF 是直角三角形;
(2)求 BE 的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com