
【题目】如图,∠AOB=120°,OP平分∠AOB,且OP=2,若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( )
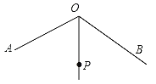
A.2个B.3个C.4个D.无数个
【答案】D
【解析】
如图在OA、OB上截取OE=OF=OP,作∠MPN=60°,只要证明△PEM≌△PON即可推出△PMN是等边三角形,由此即可得出结论.
如图在OA、OB上截取OE=OF=OP,作∠MPN=60°
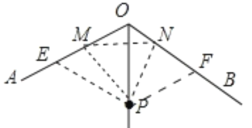
∴∠EOP=∠POF=60°,
∵OP=OE=OF,
∴△OPE,△OPF是等边三角形,
∴EP=OP,∠EPO=∠OEP=∠PON=∠MPN=60°,
∴∠EPO-∠OPM=∠MPN-∠OPM
∴∠EPM=∠OPN,
在△PEM和△PON中,
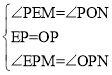
∴△PEM≌△PON(ASA).
∴PM=PN,
∵∠MPN=60°,
∴△POM是等边三角形,
∴只要∠MPN=60°,△PMN就是等边三角形,
故这样的三角形有无数个.
故选D.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】先阅读下列的解答过程,然后再解答:
形如![]() 的化简,只要我们找到两个正数a、b,使a+b=m,ab=n,使得
的化简,只要我们找到两个正数a、b,使a+b=m,ab=n,使得![]() ,
,![]() ,那么便有:
,那么便有:![]() (a>b)
(a>b)
例如:化简![]()
解:首先把![]() 化为
化为![]() ,这里m=7,n=12,由于4+3=7,4×3=12
,这里m=7,n=12,由于4+3=7,4×3=12
即![]() ,
,![]()
∴![]() =
=![]()
(1)填空:![]() = ,
= ,![]() = ;
= ;
(2)化简:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,且AD=2,AC=BC=![]() .
.
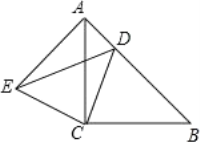
(1)证明:△ACE≌△BCD;
(2)求四边形ADCE的面积;
(3)求ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形 ABCD 中,AB=5,AD=13,点 E 为 BC 上一点,将△ABE沿 AE 折叠,使点 B 落在长方形内点 F 处,连接 DF 且 DF=12.

(1)试说明:△ADF 是直角三角形;
(2)求 BE 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
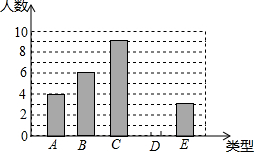
【题目】某单位750名职工积极参加向贫困地区学校捐书活动,为了解职工的捐数量,采用随机抽样的方法抽取30名职工作为样本,对他们的捐书量进行统计,统计结果共有4本、5本、6本、7本、8本五类,分别用A、B、C、D、E表示,根据统计数据绘制成了如图所示的不完整的条形统计图,由图中给出的信息解答下列问题:
(1)补全条形统计图;
(2)求这30名职工捐书本数的平均数、众数和中位数;
(3)估计该单位750名职工共捐书多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过A(-1,0)、B(4,0)、C(0,2)三点.
(1)求该二次函数的解析式;
(2)点D是该二次函数图象上的一点,且满足∠DBA=∠CAO(O是坐标原点),求点D的坐标;
(3)点P是该二次函数图象上位于一象限上的一动点,连接PA分别交BC,y轴与点E、F,若△PEB、△CEF的面积分别为S1、S2,求S1-S2的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
反比例函数y=![]() (k>0)第一象限内的图象如图1所示,点P、R是双曲线上不同的两点,过点P、R分别做PA⊥y轴于点A,RC⊥x轴于点C,两垂线交点为B.
(k>0)第一象限内的图象如图1所示,点P、R是双曲线上不同的两点,过点P、R分别做PA⊥y轴于点A,RC⊥x轴于点C,两垂线交点为B.
(1)问题提出:线段PB:PA与BR:RC有怎样的关系?
问题解决:设点PA=n,PB=m,则点P的坐标为(n,![]() ),点R的坐标为(m+n,
),点R的坐标为(m+n,![]() ),AO=BC=
),AO=BC=![]() ,RC=
,RC=![]() ,BR=
,BR=![]() ,
,
则BR:RC=![]() ,
,
PB:PA=![]() ,
,
∴PB:PA=BR:RC.
问题应用:
(2)利用上面的结论解决问题:
①如图1,如果BR=6,CR=3,AP=4,BP= .
②如图2,如果直线PR的关系式y2=﹣x+3,与x轴交于点D,与y轴交于点E,若ED=3PR,求出k的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com