
����Ŀ��Ϊ�˽�ͬѧ����ϲ��һ���ļ��е��ĸ����ڣ���ѧ����ȫУ�����ȡ����ͬѧ�����ʾ����飬���ݵ��������õ�����������������ͳ��ͼ��

����ͼ����Ϣ������������⣺
��1���˴ε���һ�������ȡ��________��ͬѧ������ͳ��ͼ�У�������������Ӧ�����ε�Բ�ĽǵĶ���Ϊ________��
��2������ѧУ��1500��ͬѧ������Ƹ�У��ϲ��������ͬѧ��������
��3���ִ���ϲ���ļ���3��ͬѧA��B��C�У����ѡ����ͬѧȥ�μ�ѧУ��֯�ġ��Ұ����족�ݽ������������б�����״ͼ�ķ�����ǡ��ѡ��A��Bȥ�μӱ����ĸ��ʣ�
���𰸡���1��120��108������2��![]() ������3��
������3��![]() ��
��
��������
��1���ɡ��ļ�������������ռ�İٷֱȵó�����ѧ�����������ɣ������������ռ�ı���������![]() ���ɵõ������
���ɵõ������
��2����ȫУѧ��������ϲ��������������ռ�������ɣ�
��3�����ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ����ѡ����2��ѧ����ǡ����A��B������������ø��ʹ�ʽ������ô𰸣�
��1����������ã�18��15%=120��������
��������ռ�ĽǶ�Ϊ36��120��360��=108����
�ʴ�Ϊ��120��108����
��2����У��ϲ��������ͬѧ������Ϊ��1500![]() ��������
��������
��3������״ͼ�ã�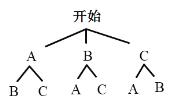
�߹���6�ֵȿ��ܵĽ����ǡ��ѡ��A��B����2�������
��ǡ��ѡ��A��B�ĸ����ǣ�![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
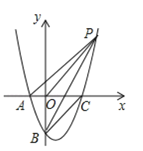
����Ŀ����֪������y=![]() x2+bx+c������A(��2��0)��B(0����4)��x�ύ����һ��C������BC��
x2+bx+c������A(��2��0)��B(0����4)��x�ύ����һ��C������BC��
��1���������ߵĽ���ʽ��
��2����ͼ��P�ǵ�һ��������������һ�㣬��![]() ����P�����꣮
����P�����꣮
��3�������������Ƿ���ڵ�D��ֱ��BD��x���ڵ�E��ʹ![]() ABE����A��B��C��E�е�����Ϊ��������������ƣ����غϣ��������ڣ��������D�����ꣻ�������ڣ���˵�����ɣ�
ABE����A��B��C��E�е�����Ϊ��������������ƣ����غϣ��������ڣ��������D�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������κ��� y=ax2+bx����a+b����a��b �dz�����a��0����
��1���жϸö��κ���ͼ���� x ��Ľ���ĸ�����˵�����ɣ�
��2�����ö��κ���ͼ�� A����1��4����B��0����1����C��1��1���������е����������㣬��ö��κ����ı���ʽ��
��3���� a+b��0���� P��2��m����m��0���ڸö��κ���ͼ���ϣ���֤��a��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ÿ���ļ�ȫ����������δ����������ˮ��ɥʧ����������ʹ�ļ���.������УΪȷ��ѧ����ȫ����չ����Զ����ˮ�䰮�������ķ���ˮ��ȫ֪ʶ����.�ִ��ߡ����꼶�и������ȡ10��ѧ���ľ����ɼ����ٷ��ƣ����������������ͷ������ɼ��÷���x��ʾ�����ֳ����飺A.80��x��85��B.85��x��90��C.90��x��95��D.95��x��100������������˲�����Ϣ��
���꼶10��ѧ���ľ����ɼ��ǣ�99��80��99��86��99��96��90��100��89��82 ��
���꼶10��ѧ���ľ����ɼ���C���е������ǣ�92��90��94.
�ߡ����꼶��ȡ��ѧ�������ɼ�ͳ�Ʊ�

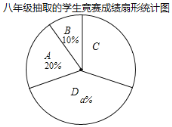
����������Ϣ������������⣺
��1������ͼ����a=______��b=______��c=______��
��2�� ��У�ߡ����꼶��400�˲μ��˴˴ξ���������ƲμӴ˴ξ�����ɼ����㣨x��90����ѧ�������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽ⱾУ���꼶ѧ������������Ŀ��400���ܡ���ѵ�������������ʦ��2019��1-5�·��ڼ䣬ÿ�������ȡ����ѧ�����в��ԣ������Գɼ���Ϊ��A��B��C��D�ĸ��ȼ�����������������ͳ��ͼ������ͳ��ͼ�ṩ����Ϣ����������⣺

��1��______�·ݲ��Ե�ѧ���������٣�______�·ݲ��Ե�ѧ����������Ů��������ȣ�
��2��������ͳ��ͼ��D�ȼ�����ռ5�·ݲ��������İٷֱȣ�
��3������У2019��5�·ݾ��꼶��Уѧ����600����������Ƴ����Գɼ���A�ȼ���ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У�ֱ��
�У�ֱ��![]() �ֱ�x�ᡢy����A��B���㣬����A��B�����������
�ֱ�x�ᡢy����A��B���㣬����A��B�����������![]() ��x����������ཻ�ڵ�
��x����������ཻ�ڵ�![]() ��
��

��1���������ߵĽ���ʽ��
��2����PΪ�߶�AB��һ�㣬![]() ����AP�ij���
����AP�ij���
��3���ڣ�2���������£���M��y����һ�㣬���ʣ����������Ƿ���ڵ�N��ʹ����A��P��M��NΪ������ı���Ϊƽ���ı��Σ������ڣ������N�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�������![]() Ϊ����)��ͼ���Ϊ
Ϊ����)��ͼ���Ϊ![]() ͼ��
ͼ��![]() ��ֱ��
��ֱ��![]() �Ľ�������Ϊ
�Ľ�������Ϊ![]() ��
��
��1������![]() ��ͼ��
��ͼ��![]() �ϣ���
�ϣ���![]() ��ֵ��
��ֵ��
��2����![]() ����Сֵ��
����Сֵ��
��3����ֱ��![]() ��ͼ���뺯��
��ͼ���뺯��![]() Ϊ����)��ͼ��ֻ��һ��������ʱ����
Ϊ����)��ͼ��ֻ��һ��������ʱ����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��4����![]() ��
��![]() ��ͼ��
��ͼ��![]() �ϣ��ҵ�
�ϣ��ҵ�![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ��
��![]() ����
����![]() ��ĶԳƵ�Ϊ��
��ĶԳƵ�Ϊ��![]() .����
.����![]() ������������ʱ���Ե�
������������ʱ���Ե�![]() Ϊ���㹹�����
Ϊ���㹹�����![]() ʹ��
ʹ��![]() ����
����![]() ����.��ͼ��
����.��ͼ��![]() �����
�����![]() �ı�������������ʱ��ֱ��д��
�ı�������������ʱ��ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ�κ��ʱ����������ѧ�������ڡ�����������������ˡ���Բ��������֮��ϸ����ʧ���٣���֮�ָ�������ɸ����Բ�ܺ��壬������ʧҲ����Ҳ��������Բ���ڽӶ�����ƽ�Բ�ķ��������Ƽ���Բ��������ܳ�����ͼ1������Բ���ڽ��������ε����![]() �����ƹ��ư뾶Ϊ1�ġ�O�������������ͼ2��Բ���ڽ���ʮ�����ε����
�����ƹ��ư뾶Ϊ1�ġ�O�������������ͼ2��Բ���ڽ���ʮ�����ε����![]() �����ƹ��ư뾶Ϊ1�ġ�O���������
�����ƹ��ư뾶Ϊ1�ġ�O���������![]() ____��(�����������)
____��(�����������)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��C������ABCD����������B��A��D������BD������A��AE��BD������CB�ڵ�E��
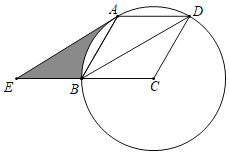
��1����֤��AE����C�����ߣ�
��2�����뾶Ϊ2����ͼ���߶�AE���߶�BE��![]() Χ�ɵIJ��ֵ������
Χ�ɵIJ��ֵ������
��3���ڣ�2���������£�����C��ȡ��F������AF��ʹ��DAF��15�㣬���F��ֱ��AD�ľ��룮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com