
【题目】(2017黑龙江省绥化市)已知关于x的一元二次方程![]() .
.
(1)当m为何值时,方程有两个不相等的实数根?
(2)若边长为5的菱形的两条对角线的长分别为方程两根的2倍,求m的值.
【答案】(1)m>﹣![]() ;(2)m=﹣4.
;(2)m=﹣4.
【解析】试题(1)根据方程的系数结合根的判别式,即可得出△=4m+17>0,解之即可得出结论;
(2)设方程的两根分别为a、b,根据根与系数的关系结合菱形的性质,即可得出关于m的一元二次方程,解之即可得出m的值,再根据a+b=﹣2m﹣1>0,即可确定m的值.
试题解析:(1)∵方程![]() 有两个不相等的实数根,∴△=
有两个不相等的实数根,∴△=![]() =4m+17>0,解得:m>﹣
=4m+17>0,解得:m>﹣![]() ,∴当m>﹣
,∴当m>﹣![]() 时,方程有两个不相等的实数根.
时,方程有两个不相等的实数根.
(2)设方程的两根分别为a、b,根据题意得:a+b=﹣2m﹣1,ab=![]() .
.
∵2a、2b为边长为5的菱形的两条对角线的长,∴![]() =
=![]() =2m2+4m+9=52=25,解得:m=﹣4或m=2.
=2m2+4m+9=52=25,解得:m=﹣4或m=2.
∵a>0,b>0,∴a+b=﹣2m﹣1>0,∴m=﹣4.
若边长为5的菱形的两条对角线的长分别为方程两根的2倍,则m的值为﹣4.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:
【题目】在“母亲节”前期,某花店购进康乃馨和玫瑰两种鲜花,销售过程中发现康乃馨比玫瑰销售量大,店主决定将玫瑰每枝降价1元促销,降价后30元可购买玫瑰的数量是原来购买玫瑰数量的1.5倍.
(1)求降价后每枝玫瑰的售价是多少元?
(2)根据销售情况,店主用不多于900元的资金再次购进两种鲜花共500枝,康乃馨进价为2元/枝,玫瑰进价为1.5元/枝,问至少购进玫瑰多少枝?
查看答案和解析>>
科目:初中数学 来源: 题型:
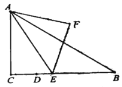
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一定点,且
边上一定点,且![]() ,点
,点![]() 是线段
是线段![]() 上一动点,连接
上一动点,连接![]() ,以
,以![]() 为斜边在
为斜边在![]() 的右侧作等腰直角
的右侧作等腰直角![]() .当点
.当点![]() 从点
从点![]() 出发运动至点
出发运动至点![]() 停止时,点
停止时,点![]() 的运动的路径长为_________.
的运动的路径长为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=(2m+4)x+(3﹣n).
(1)当m、n是什么数时,y随x的增大而增大;
(2)当m、n是什么数时,函数图象经过原点;
(3)若图象经过一、二、三象限,求m、n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
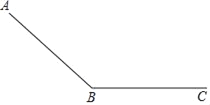
【题目】如图,一个滑道由滑坡(AB段)和缓冲带(BC段)组成,滑雪者在滑坡上滑行的距离y1(单位:m)和滑行时间t1(单位s)满足二次函数关系,并测得相关数据:
滑行时间t1/s | 0 | 1 | 2 | 3 | 4 |
滑行距离y1/s | 0 | 4.5 | 14 | 28.5 | 48 |
滑雪者在缓冲带上滑行的距离y2(单位:m)和滑行时间t2(单位:s)满足:y2=52t2﹣2t22,滑雪者从A出发在缓冲带BC上停止,一共用了23s.
(1)求y1和t1满足的二次函数解析式;
(2)求滑坡AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB,标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,求建筑物的高.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线y1=x2﹣4x+4的顶点为A,直线y2=kx﹣2k(k≠0),
(1)试说明直线是否经过抛物线顶点A;
(2)若直线y2交抛物线于点B,且△OAB面积为1时,求B点坐标;
(3)过x轴上的一点M(t,0)(0≤t≤2),作x轴的垂线,分别交y1,y2的图象于点P,Q,判断下列说法是否正确,并说明理由:
①当k>0时,存在实数t(0≤t≤2)使得PQ=3.
②当﹣2<k<﹣0.5时,不存在满足条件的t(0≤t≤2)使得PQ=3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l1:![]() 过点A(3,0),且与直线l2:
过点A(3,0),且与直线l2:![]() 交于点B(m,1).
交于点B(m,1).
(1)求直线l1:![]() 的函数表达式;
的函数表达式;
(2)过动点P(n,0)且垂于x轴的直线与l1、l2分别交于点C、D,当点C位于点D上方时,直接写出n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com