
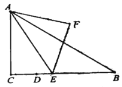
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一定点,且
边上一定点,且![]() ,点
,点![]() 是线段
是线段![]() 上一动点,连接
上一动点,连接![]() ,以
,以![]() 为斜边在
为斜边在![]() 的右侧作等腰直角
的右侧作等腰直角![]() .当点
.当点![]() 从点
从点![]() 出发运动至点
出发运动至点![]() 停止时,点
停止时,点![]() 的运动的路径长为_________.
的运动的路径长为_________.
【答案】![]()
【解析】
如图,连接CF,作FM⊥BC于M,FN⊥AC于N.证明△FNA≌△FME(AAS),推出FM=FM,AN=EM,推出四边形CMFN是正方形,推出点F在射线CF上运动(CF是∠ACB的角平分线),求出两种特殊位置CF的长即可解决问题.
如图,连接CF,作FM⊥BC于M,FN⊥AC于N.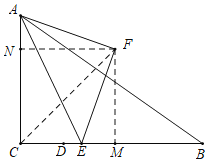
∵∠FNC=∠MCN=∠FMC=90°,
∴四边形CMFN是矩形,
∴∠MFN=∠AFE=90°,
∴∠AFN=∠MFE,
∵AF=FE,∠FNA=∠FME=90°,
∴△FNA≌△FME(AAS),
∴FM=FM,AN=EM,
∴四边形CMFN是正方形,
∴CN=CM,CF=![]() CM,∠FCN=∠FCM=45°,
CM,∠FCN=∠FCM=45°,
∵AC+CE=CN+AN+CM-EM=2CM,
∴CF=![]() (AC+CE).
(AC+CE).
∴点F在射线CF上运动(CF是∠ACB的角平分线),
当点E与D重合时,CF=![]() (AC+CD)=2
(AC+CD)=2![]() ,
,
当点E与B重合时,CF=![]() (AC+CB)=
(AC+CB)=![]() ,
,
∵![]() -2
-2![]() =
=![]() ,
,
∴点F的运动的路径长为![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】已知,在正方形 ABCD 中,AB=5,点 F 是边 DC 上的一个动点,将△ADF 绕点 A 顺时针旋转 90°至△ABE,点 F 的对应点 E 落在 CB 的延长线上,连接 EF.
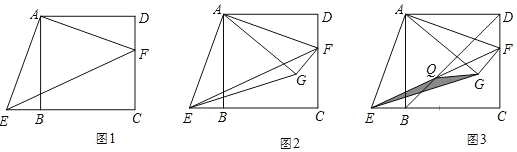
(1)如图 1,求证:∠DAF+∠FEC=∠AEF;
(2)将△ADF 沿 AF 翻折至△AGF,连接 EG.
①如图 2,若 DF=2,求 EG 的长;
②如图 3,连接 BD 交 EF 于点 Q,连接 GQ,则 S△QEG 的最大值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
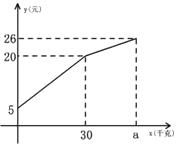
【题目】一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题.
(1)农民自带的零钱是多少?
(2)试求降价前y与x之间的关系式
(3)由表达式你能求出降价前每千克的土豆价格是多少?
(4)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:点![]() 关于原点的对称点为
关于原点的对称点为![]() ,以
,以![]() 为边作等边
为边作等边![]() ,则称点
,则称点![]() 为
为![]() 的“等边对称点”;
的“等边对称点”;
(1)若![]() ,求点
,求点![]() 的“等边对称点”的坐标;
的“等边对称点”的坐标;
(2)若![]() 点是双曲线
点是双曲线![]() 上动点,当点
上动点,当点![]() 的“等边对称点”点
的“等边对称点”点![]() 在第四象限时,
在第四象限时,
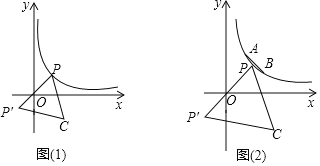
①如图(1),请问点![]() 是否也会在某一函数图象上运动?如果是,请求出此函数的解析式;如果不是,请说明理由;
是否也会在某一函数图象上运动?如果是,请求出此函数的解析式;如果不是,请说明理由;
②如图(2),已知点![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上的动点,点
上的动点,点![]() 在
在![]() 轴上,若以
轴上,若以![]() 、
、![]() 、
、![]() 、
、![]() 这四个点为顶点的四边形是平行四边形时,求点
这四个点为顶点的四边形是平行四边形时,求点![]() 的纵坐标
的纵坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
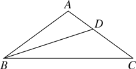
【题目】如图,在△ABC中,AB=AC,∠A=108°,BD平分∠ABC交AC于点D.
(1)填空:∠DBC=_________度;
(2)猜想:BC、AB、CD三者数量关系_____________________;
(3)证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
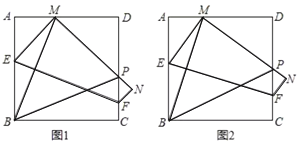
【题目】如图1.在边长为10的正方形![]() 中,点
中,点![]() 在边
在边![]() 上移动(点
上移动(点![]() 不与点
不与点![]() ,
,![]() 重合),
重合),![]() 的垂直平分线分别交
的垂直平分线分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,将正方形
,将正方形![]() 沿
沿![]() 所在直线折叠,则点
所在直线折叠,则点![]() 的对应点为点
的对应点为点![]() ,点
,点![]() 落在点
落在点![]() 处,
处,![]() 与
与![]() 交于点
交于点![]() ,
,
(1)若![]() ,求
,求![]() 的长;
的长;
(2)随着点![]() 在边
在边![]() 上位置的变化,
上位置的变化,![]() 的度数是否发生变化?若变化,请说明理由;若不变,请求出
的度数是否发生变化?若变化,请说明理由;若不变,请求出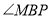 的度数;
的度数;
(3)随着点![]() 在边
在边![]() 上位置的变化,点
上位置的变化,点![]() 在边
在边![]() 上位置也发生变化,若点
上位置也发生变化,若点![]() 恰好为
恰好为![]() 的中点(如图2),求
的中点(如图2),求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔赛跑”是同学们熟悉的寓言故事.如图所示,表示了寓言中的龟、兔的路程S和时间t的关系(其中直线段表示乌龟,折线段表示兔子).下列叙述正确的是( )

A. 赛跑中,兔子共休息了50分钟
B. 乌龟在这次比赛中的平均速度是0.1米/分钟
C. 兔子比乌龟早到达终点10分钟
D. 乌龟追上兔子用了20分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017黑龙江省绥化市)已知关于x的一元二次方程![]() .
.
(1)当m为何值时,方程有两个不相等的实数根?
(2)若边长为5的菱形的两条对角线的长分别为方程两根的2倍,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于两点A,B,给出如下定义:以线段AB为边的正方形称为点A,B的“确定正方形”.如图为点A,B 的“确定正方形”的示意图.
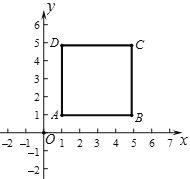
(1)如果点M的坐标为(0,1),点N的坐标为(3,1),那么点M,N的“确定正方形”的面积为___________;
(2)已知点O的坐标为(0,0),点C为直线![]() 上一动点,当点O,C的“确定正方形”的面积最小,且最小面积为2时,求b的值.
上一动点,当点O,C的“确定正方形”的面积最小,且最小面积为2时,求b的值.
(3)已知点E在以边长为2的正方形的边上,且该正方形的边与两坐标轴平行,对角线交点为P(m,0),点F在直线![]() 上,若要使所有点E,F的“确定正方形”的面积都不小于2,直接写出m的取值范围.
上,若要使所有点E,F的“确定正方形”的面积都不小于2,直接写出m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com