
 如图,在⊙O中,AB为弦,且AB⊥OP于D,PA为⊙O的切线,AB=8cm,OD=3cm,则PA的长为
如图,在⊙O中,AB为弦,且AB⊥OP于D,PA为⊙O的切线,AB=8cm,OD=3cm,则PA的长为| 1 |
| 2 |
| 1 |
| 2 |
| AD2+OD2 |
| 42+32 |
| PA |
| OA |
| AD |
| OD |
| PA |
| 5 |
| 4 |
| 3 |
| 20 |
| 3 |
| 20 |
| 3 |


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
 若用A、B、C、分别表示有理数a、b、c,0为原点,如图所示.已知a<c<0,b>0.
若用A、B、C、分别表示有理数a、b、c,0为原点,如图所示.已知a<c<0,b>0.查看答案和解析>>
科目:初中数学 来源: 题型:
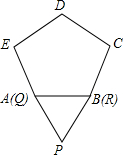 如图,将边长为1的等边△PQR沿着边长为1的正五边形ABCDE外部的边连续滚动(点Q、点R分别与点A、点B重合),当△PQR第一次回到原来的起始位置时(顶点位置与原来相同),点P所经过的路线长为
如图,将边长为1的等边△PQR沿着边长为1的正五边形ABCDE外部的边连续滚动(点Q、点R分别与点A、点B重合),当△PQR第一次回到原来的起始位置时(顶点位置与原来相同),点P所经过的路线长为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com