
如图(1),抛物线 与x轴交于A、B两点,与y轴交于点C,其中点A的坐标为(﹣2,0).
与x轴交于A、B两点,与y轴交于点C,其中点A的坐标为(﹣2,0).
(1)求此抛物线的解析式;
(2)①若点D是第一象限内抛物线上的一个动点,过点D作DE⊥x轴于E,连接CD,以OE为直径作⊙M,如图(2),试求当CD与⊙M相切时D点的坐标;
②点F是x轴上的动点,在抛物线上是否存在一点G,使A、C、G、F四点为顶点的四边形是平行四边形?若存在,求出点G的坐标;若不存在,请说明理由.

(1) ;
;
(2)①( ,
, );②存在,(4,3)或(
);②存在,(4,3)或( )或(
)或( ).
).
【解析】
试题分析:(1)把A的坐标代入抛物线的解析式,即可得到关于c的方程,求的c的值,则抛物线的解析式即可求解.
(2)①连接MC、MD,证明△COM∽△MED,根据相似三角形的对应边的比相等即可求解.
②分四种情况进行讨论,根据平行四边形的性质即可求解.
试题解析:【解析】
(1)∵点A(﹣2,0)在抛物线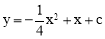 上,
上,
∴ ,解得c=3.
,解得c=3.
∴抛物线的解析式是: .
.
(2)①令D(x,y),(x>0,y>0),则E(x,0),M( ,0),
,0),
由(1)知C(0,3),
如答图1,连接MC、MD
∵DE、CD与⊙O相切,∴∠CMD=90°.
∴△COM∽△MED. ∴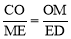 ,即
,即 .
.
又∵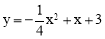 ,∴
,∴ ,解得x=
,解得x= .
.
又∵x>0,∴x= ,∴
,∴ .
.
∴D点的坐标是:( ,
, ).
).

②假设存在满足条件的点G(a,b).
若构成的四边形是□ACGF,(答图2)则G与C关于直线x=2对称,
∴G点的坐标是:(4,3).
若构成的四边形是□ACFG,(答图3,4)则由平行四边形的性质有b= ,
,
又∵ ,解得a=
,解得a= ,此时G点的坐标是:(
,此时G点的坐标是:( ).
).
若构成的四边形是□AGCF,(答图5)则CG FA,
FA,
∴G点的坐标是:(4,3).
显而易见,AFCG不能构成平行四边形.
综上所述,在抛物线上存在点G,使A、C、G、F四点为顶点的四边形是平行四边形,点G的坐标为(4,3)或( )或(
)或( ).
).

考点:1.单动点问题;2.二次函数综合题;3.曲线上点的坐标与方程的关系;4.直线与圆相切的性质;5.相似三角形的判定和性质;6. 平行四边形的性质;7.分类思想的应用.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源:2014年初中毕业升学考试(广西桂林卷)数学(解析版) 题型:填空题
观察下列运算:81=8,82=64,83=512,84=4096,85=32768,86=262144,…,则:81+82+83+84+…+82014的和的个位数字是 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西崇左卷)数学(解析版) 题型:选择题
震惊世界的MH370失联事件发生后第30天,中国“海巡01”轮在南印度洋海域搜索过程中,首次侦听到疑是飞机黑匣子的脉冲信号,探测到的信号所在海域水深4500米左右,其中4500用科学记数法表示为( )
A.4.5×102 B.4.5×103 C.45.0×102 D.0.45×104
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西南宁卷)数学(解析版) 题型:选择题
已知点A在双曲线
 上,点B在直线
上,点B在直线 上,且A,B两点关于
上,且A,B两点关于 轴对称,设点A的坐标为(
轴对称,设点A的坐标为( ,
, ),则
),则 +
+ 的值是( )
的值是( )
(A)-10 (B)-8 (C)6 (D)4
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西北海卷)数学(解析版) 题型:解答题
经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,这三种可能性大小相同,现在两辆汽车经过这个十字路口.
(1)请用“树形图”或“列表法”列举出这两辆汽车行驶方向所有可能的结果;
(2)求这两辆汽车都向左转的概率.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广东汕尾卷)数学(解析版) 题型:解答题
已知关于x的方程 .
.
(1)若该方程的一个根为1,求a的值及该方程的另一根;
(2)求证:不论a取何实数,该方程都有两个不相等的实数根.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广东梅州卷)数学(解析版) 题型:选择题
若x>y,则下列式子中错误的是( )
A、x-3>y-3 B、 C、x+3>y+3 D、-3x>-3y
C、x+3>y+3 D、-3x>-3y
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com