
【题目】(4分)有一组数据:3,4,5,6,6,则这组数据的平均数、众数、中位数分别是( )
A.4.8,6,6 B.5,5,5 C.4.8,6,5 D.5,6,6
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
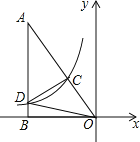
【题目】如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=![]() (x<0)经过斜边OA上的点C,且OC:AC=1:2,与另一直角边交于点D,若S△OCD=12,则k= .
(x<0)经过斜边OA上的点C,且OC:AC=1:2,与另一直角边交于点D,若S△OCD=12,则k= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的个数是( )
①任何有理数的偶次幂都是正数;②倒数等于本身的数有0,-1和1;③用一个平面截正方体最多得到六边形;④所有有理数都能用数轴上的点表示;⑤整式包括单项式和多项式
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
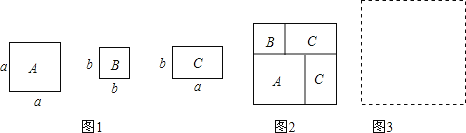
【题目】现有若干张如图1的正方形硬纸片A.B和长方形硬纸片C.
(1)小明利用这些硬纸片拼成了如图2的一个新正方形,用两种不同的方法,计算出了新正方形的面积,由此,他得到了一个等式:_____________
(2)小明再取其中的若干张(三种纸片都取到)拼成一个面积为a2+nab+2b2长方形,则n可取的正整数值为____,并请在图3位置画出拼成的图形。
(3)根据拼图的经验,请将多项式a2+4ab+3b2分解因式:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上林老师出示了问题:如图,AD∥BC,∠AEF=90°,AD=AB=BC=DC,∠B=90°,点E是边BC的中点,且EF交∠DCG的平分线CF于点F,求证:AE=EF.
同学们作了一步又一步的研究:
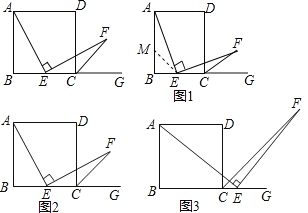
(1)经过思考,小明展示了一种解题思路:如图1,取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF,小明的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)小颖提出一个新的想法:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(3)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平静的湖面上,有一支红莲,高出水面1米,一阵风吹来,红莲移到一边,花朵齐及水面,已知红莲移动的水平距离为2米,这里的水深为( )米.
A.1.5
B.2
C.2.5
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
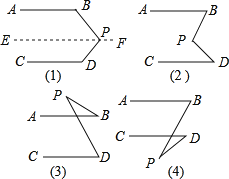
【题目】如图(1),AB∥CD,猜想∠BPD与∠B、∠D的关系,说出理由.
解:猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°(两直线平行,同旁内角互补)
∵AB∥CD,EF∥AB,
∴EF∥CD,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行.)
∴∠EPD+∠D=180°(两直线平行,同旁内角互补)
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
(1)依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的关系,并说明理由.
(2)观察图(3)和(4),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的关系,不需要说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com