
【题目】已知:如图,点P是数轴上表示-2与-1两数的点为端点的线段的中点.
![]()
(1)数轴上点P表示的数为 ;
(2)在数轴上距离点P为2.5个单位长度的点表示的数为 ;
(3)如图,若点P是线段AB(点A在点B的左侧)的中点,且点A表示的数为m,那么点B表示的数是 .(用含m的代数式表示)
【答案】(1)-1.5;(2)1或-4;(3)-3-m.
【解析】
(1)设点P表示的数为x.根据点P是数轴上表示-2与-1两数的点为端点的线段的中点,得到-1-x=x-(-2),解方程即可;
(2)设点P表示的数为x.则![]() ,解方程即可;
,解方程即可;
(3)设B表示的数为y,则m+y=2×(-1.5),求出y的表达式即可.
(1)设点P表示的数为x.
∵点P是数轴上表示-2与-1两数的点为端点的线段的中点,
∴-1-x=x-(-2),
解得:x=-1.5.
故答案为:-1.5.
(2)设点P表示的数为x.则![]() ,
,
∴![]() ,
,
∴x+1.5=±2.5,
∴x+1.5=2.5或x+1.5=-2.5
∴x=1或x=-4.
(3)设B表示的数为y,则m+y=2×(-1.5),
∴m+y=-3,
∴y=-3-m.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
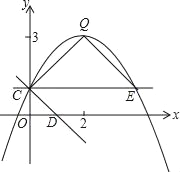
【题目】如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,且OD=OC.
(1)求直线CD的解析式;
(2)求抛物线的解析式;
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,求证:△CEQ∽△CDO;
(4)在(3)的条件下,若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简与求值
(1)求3x2+x+3(x2﹣![]() x)﹣(6x2+x)的值,其中x=﹣6.
x)﹣(6x2+x)的值,其中x=﹣6.
(2)先化简,再求值:5(3a2b﹣ab2)﹣4(﹣ab2+3a2b),其中|a+1|+(b﹣![]() )2=0
)2=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以四边形ABCD的边AB、AD为底边分别作等腰三角形ABE和等腰三角形ADF.
(1)当四边形ABCD为正方形时(如图①),以边AB、AD为斜边分别向外侧作等腰直角△ABE和等腰直角△ADF,连接BF、ED,线段BF和ED的数量关系是_____________;
(2)当四边形ABCD为矩形时(如图②),以边AB、AD为斜边分别向矩形内侧、外侧作等腰直角△ABE和等腰直角△ADF,连接EF、BD,线段EF和BD具有怎样的数量关系?请说明理由;
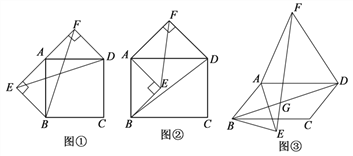
(3)当四边形ABCD为平行四边形时,以边AB、AD为底边分别向平行四边形内侧、外侧作等腰△ABE和等腰△ADF,且△ABE和△ADF的顶角均为![]() ,连接EF、BD,交点为G.请用
,连接EF、BD,交点为G.请用![]() 表示出∠FGD,并说明理由.
表示出∠FGD,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等边三角形,D是BC边上的一个动点(点D不与B,C重合)△ADF是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.

(1)如图1,求证:△AFB≌△ADC;
(2)请判断图1中四边形BCEF的形状,并说明理由;
(3)若D点在BC 边的延长线上,如图2,其它条件不变,请问(2)中结论还成立吗?如果成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)停车难已成为合肥城市病之一,主要表现在居住停车位不足,停车资源结构性失衡,中心城区供需差距大等等.如图是张老师的车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米,已知小汽车车门宽AO为 1.2 米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?请说明理由.(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】华润苏果超市有A、B、C三种果冻出售,A种果冻20千克,售价为m元每千克,B种果冻60千克,售价比A种贵2元每千克,C种果冻40千克,售价比A种便宜1元每千克.
(1)若将这三种果冻全部混合在一起销售,在保证总售价不变的情况下,混合果冻的售价应定为多少?
(2)售货员小张在写混合后的销售单价牌时,误写成原来三个单价的平均数,如果混合果冻按小张写的单价全部售完,超市的这批果冻的利润有何变化?变化多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式了的平方,如3+2![]() =(1+
=(1+![]() )2.善于思考的小明进行了以下探索:
)2.善于思考的小明进行了以下探索:
若设a+b![]() =(m+n
=(m+n![]() )2=m2+2n2+2mn
)2=m2+2n2+2mn![]() (其中a、b、m、n均为整数),
(其中a、b、m、n均为整数),
则有a=m2+2n2,b=2mn.
这样小明就找到了一种把类似a+b![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)若a+b![]() =(m+n
=(m+n![]() )2,当a、b、m、n均为整数时,用含m、n的式子分别表示a、b,得:a= ,b= ;
)2,当a、b、m、n均为整数时,用含m、n的式子分别表示a、b,得:a= ,b= ;
(2)若a+6![]() =(m+n
=(m+n![]() )2,且a、m、n均为正整数,求a的值;
)2,且a、m、n均为正整数,求a的值;
(3)化简:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com