
【题目】化简与求值
(1)求3x2+x+3(x2﹣![]() x)﹣(6x2+x)的值,其中x=﹣6.
x)﹣(6x2+x)的值,其中x=﹣6.
(2)先化简,再求值:5(3a2b﹣ab2)﹣4(﹣ab2+3a2b),其中|a+1|+(b﹣![]() )2=0
)2=0
科目:初中数学 来源: 题型:
【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
调查结果统计表
组别 | 分组(单位:元) | 人数 |
A | 0≤x<30 | 4 |
B | 30≤x<60 | 16 |
C | 60≤x<90 | a |
D | 90≤x<120 | b |
E | x≥120 | 2 |
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有__人,a+b=__,m=___;
(2)求扇形统计图中扇形C的圆心角度数;
(3)该校共有学生1000人,请估计每月零花钱的数额x在60≤x<120范围的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
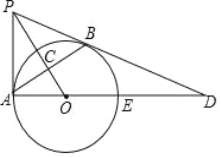
【题目】如图,PB与⊙O相切于点B,过点B作OP的垂线BA,垂足为C,交⊙O于点A,连结PA,AO,AO的延长线交⊙O于点E,与PB的延长线交于点D.
(1)求证:PA是⊙O的切线;
(2)若tan∠BAD=![]() ,且OC=4,求BD的长.
,且OC=4,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
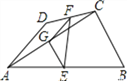
【题目】如图,四边形 ABCD 中,AD=BC,E、F、G 分别是 AB、CD、AC 的中点,若∠DAC=20 ,∠ACB=90 ,则 ∠FEG=( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形 ABCD 中, G 为 BC 边上一点, BE AG 于 E , DF AG 于 F ,连接 DE .
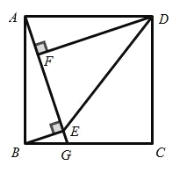
(1)求证: ABE DAF ;
(2)若 AF 1,四边形 ABED 的面积为6 ,求 EF 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线 y 2x 4 与 x 轴、 y 轴分别交于 A 、 B 两点.
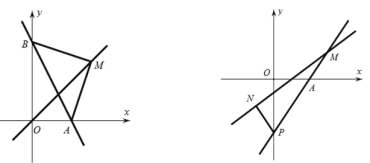
(1)求 A 、 B 两点的坐标;
(2)若点 M 为直线 y mx 上一点,且ABM 是等腰直角三角形,求 m 的值;
(3)过 A 点的直线 y kx 2k 交 y 轴负半轴于 P ,N 点的横坐标为1,过 N 点的直线![]() 于点 M ,试探究 PM 与 PN 之间的数量关系.
于点 M ,试探究 PM 与 PN 之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足CF∶DF=1∶3,连接AF并延长交⊙O于点E,连接AD、DE,若CF=3,AF=4.
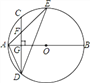
(1)求证:△ADF∽△AED;
(2)求FG的长;
(3)求tan∠E的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点P是数轴上表示-2与-1两数的点为端点的线段的中点.
![]()
(1)数轴上点P表示的数为 ;
(2)在数轴上距离点P为2.5个单位长度的点表示的数为 ;
(3)如图,若点P是线段AB(点A在点B的左侧)的中点,且点A表示的数为m,那么点B表示的数是 .(用含m的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了更好的开展“学校特色体育教育”,从全校八年级的各班分别随机抽取了5名男生和5名女生,组成了一个容量为60的样本,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:某校60名学生体育测试成绩频数分布表
成绩 | 划记 | 频数 | 百分比 |
优秀 | 正正正 | a | 30% |
良好 | 正正正正正正 | 30 | b |
合格 | 正 | 9 | 15% |
不合格 |
| 3 | 5% |
合计 | 60 | 60 | 100% |
(说明:40﹣﹣﹣55分为不合格,55﹣﹣﹣70分为合格,70﹣﹣﹣85分为良好,85﹣﹣﹣100分为优秀)请根据以上信息,解答下列问题:
(1)表中的a=_____,b=_____;
(2)请根据频数分布表,画出相应的频数分布直方图;
(3)如果该校八年级共有150名学生,根据以上数据,估计该校八年级学生身体素质良好及以上的人数为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com