
【题目】如图,在平面直角坐标系中,直线 y 2x 4 与 x 轴、 y 轴分别交于 A 、 B 两点.
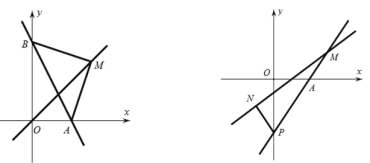
(1)求 A 、 B 两点的坐标;
(2)若点 M 为直线 y mx 上一点,且ABM 是等腰直角三角形,求 m 的值;
(3)过 A 点的直线 y kx 2k 交 y 轴负半轴于 P ,N 点的横坐标为1,过 N 点的直线![]() 于点 M ,试探究 PM 与 PN 之间的数量关系.
于点 M ,试探究 PM 与 PN 之间的数量关系.
【答案】(1)![]() ;(2)当m>0时,m的值为1或
;(2)当m>0时,m的值为1或![]() 或
或![]() ;当m<0时,m的值为:-
;当m<0时,m的值为:-![]() 或-2;(3)
或-2;(3)![]()
【解析】
(1)根据直线 y 2x 4 与 x 轴、 y 轴分别交于 A 、 B 两点,分别令y=0 ,x=0,求出即可;
(2)当BM⊥BA,且BM=BA时,过M作MN⊥y轴于N,证△BMN≌△ABO(AAS),求出M的值即可;②当AM⊥BA,且AM=BA时,过M作MN⊥x轴于N,同法求出M的值;③当AM⊥BM,且AM=BM时,过M作MN⊥x轴于N,MH⊥y轴于H,证△BHM≌△AMN,求出M的值即可.
(3)设NM与x轴的交点为H,分别过M、H作x轴的垂线垂足为G,HD交MP于D点,求出H、G的坐标,证△AMG≌△ADH,△AMG≌△ADH≌△DPC≌△NPC,推出PN=PD=AD=AM代入即可求出答案.
解:(1)y 2x 4 与 x 轴、 y 轴分别交于 A 、 B 两点
令y=0,则x=2; 令x=0,则y=4![]()
![]()
(2) (i)当m>0时,分三种情况:
①如图1,
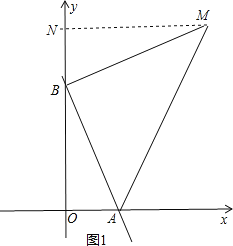
当BM⊥BA,且BM=BA时,过M作MN⊥y轴于N,
∵BM⊥BA,MN⊥y轴,OB⊥OA,
∴∠MBA=∠MNB=∠BOA=90°,
∴∠NBM+∠NMB=90°,∠ABO+∠NBM=90°,
∴∠ABO=∠NMB,
在△BMN和△ABO中,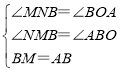 ,
,
∴△BMN≌△ABO(AAS),
MN=OB=4,BN=OA=2,
∴ON=2+4=6,
∴M的坐标为(4,6),
代入y=mx得:m=![]() ,
,
②如图2,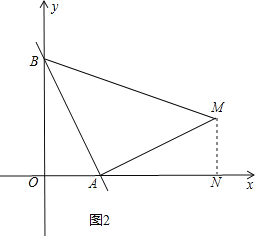
当AM⊥BA,且AM=BA时,过M作MN⊥x轴于N,△BOA≌△ANM(AAS),同理求出M的坐标为(6,2),m=![]() ,
,
③如图4,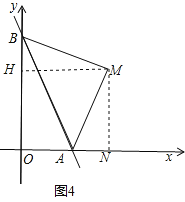
当AM⊥BM,且AM=BM时,过M作MN⊥X轴于N,MH⊥Y轴于H,则△BHM≌△AMN,
∴MN=MH,
设M(x,x)代入y=mx得:x=mx,
∴m=1,
答:m的值是![]() 或
或![]() 或1;
或1;
(ii)当m<0时,由(i)得:关于直线AB:y=-2x+4,
同理可得:m=-![]() 或-2;
或-2;
(3)解:如图,
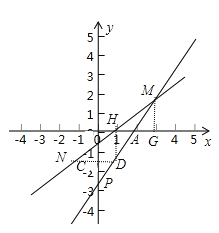
设NM与x轴的交点为H,过M作![]() 轴于G,过H作
轴于G,过H作![]() 轴,HD交MP于D点,连接ND,
轴,HD交MP于D点,连接ND,
由![]() 与x轴交于H点,
与x轴交于H点,![]() ,
,
由![]() 与
与![]() 交于M点,
交于M点,![]() ,
,
而![]() ,
,![]() 为HG的中点,
为HG的中点,![]() ,
,
又![]() N点的横坐标为-1,且在
N点的横坐标为-1,且在![]() 上,可得N 的纵坐标为-k,同理P的纵坐标为
上,可得N 的纵坐标为-k,同理P的纵坐标为![]() ,
,![]() 平行于x轴,且N、D的横坐标分别为-1、1
平行于x轴,且N、D的横坐标分别为-1、1![]() 与D关于y轴对称,
与D关于y轴对称,![]() ,
,![]() ,
,![]()
![]()
![]()


科目:初中数学 来源: 题型:
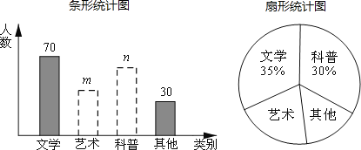
【题目】在“书香包河”读书活动中,学校准备购买一批课外读物,为使课外读物满足学生们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根据调查结果绘制的两幅不完整的统计图.请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了______________名同学;
(2)条形统计图中,m=_________,n=__________;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
快放寒假了,小宇来到书店准备购买一些课外读物在假期里阅读.在选完书结账时,收银员告诉小宇,如果花20元办理一张会员卡,用会员卡结账买书,可以享受8折优惠.小宇心算了一下,觉得这样可以节省13元,很合算,于是采纳了收银员的意见.请根据以上信息解答下列问题:
(1)你认为小宇购买 元以上的书,办卡就合算了;
(2)小宇购买这些书的原价是多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行了调查,随机调查了![]() 人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.

(1)根据图中信息求出![]() =___________,
=___________,![]() =_____________;
=_____________;
(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生种,大约有多少人最认可“微信”这一新生事物?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简与求值
(1)求3x2+x+3(x2﹣![]() x)﹣(6x2+x)的值,其中x=﹣6.
x)﹣(6x2+x)的值,其中x=﹣6.
(2)先化简,再求值:5(3a2b﹣ab2)﹣4(﹣ab2+3a2b),其中|a+1|+(b﹣![]() )2=0
)2=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组数0,2,4,8,12,18,…中的奇数项和偶数项分别用代数式![]() ,
,![]() 表示,如第1个数为
表示,如第1个数为![]() ,第2个数为
,第2个数为![]() ,第3个数为
,第3个数为![]() ,…,则第8个数的值是_____,数轴上现有一点
,…,则第8个数的值是_____,数轴上现有一点![]() 从原点出发,依次以此组数中的数为距离向左右来回跳跃.第1秒时,点
从原点出发,依次以此组数中的数为距离向左右来回跳跃.第1秒时,点![]() 在原点,记为
在原点,记为![]() ;第2秒点
;第2秒点![]() 向左跳2个单位,记为
向左跳2个单位,记为![]() ,此时点
,此时点![]() 表示的数为-2;第3秒点
表示的数为-2;第3秒点![]() 向右跳4个单位,记为
向右跳4个单位,记为![]() ,点
,点![]() 表示的数为2;…按此规律跳跃,点
表示的数为2;…按此规律跳跃,点![]() 表示的数为_______.
表示的数为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以四边形ABCD的边AB、AD为底边分别作等腰三角形ABE和等腰三角形ADF.
(1)当四边形ABCD为正方形时(如图①),以边AB、AD为斜边分别向外侧作等腰直角△ABE和等腰直角△ADF,连接BF、ED,线段BF和ED的数量关系是_____________;
(2)当四边形ABCD为矩形时(如图②),以边AB、AD为斜边分别向矩形内侧、外侧作等腰直角△ABE和等腰直角△ADF,连接EF、BD,线段EF和BD具有怎样的数量关系?请说明理由;
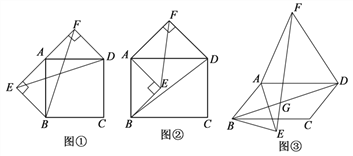
(3)当四边形ABCD为平行四边形时,以边AB、AD为底边分别向平行四边形内侧、外侧作等腰△ABE和等腰△ADF,且△ABE和△ADF的顶角均为![]() ,连接EF、BD,交点为G.请用
,连接EF、BD,交点为G.请用![]() 表示出∠FGD,并说明理由.
表示出∠FGD,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)停车难已成为合肥城市病之一,主要表现在居住停车位不足,停车资源结构性失衡,中心城区供需差距大等等.如图是张老师的车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米,已知小汽车车门宽AO为 1.2 米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?请说明理由.(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=90°,点D在射线BC上(与B、C两点不重合),以AD为边作正方形ADEF,使点E与点B在直线AD的异侧,射线BA与射线CF相交于点G.
(1)若点D在线段BC上,如图1.
①依题意补全图1;
②判断BC与CG的数量关系与位置关系,并加以证明;
(2)若点D在线段BC的延长线上,且G为CF中点,连接GE,AB=![]() ,则GE的长为_____,并简述求GE长的思路.
,则GE的长为_____,并简述求GE长的思路.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com