
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y=ax2+bx+c��ԭ��O��B����4��4�����ҶԳ���Ϊֱ��x=![]() ��
��
��1���������ߵĺ�������ʽ��
��2��D��ֱ��OB�·��������ϵ�һ���㣬����OD��BD���ڵ�D�˶������У�����OBD������ʱ�����D���������OBD����������
��3����ͼ2������PΪƽ����һ�㣬��N���������ϣ��ҡ�NBO=��ABO�����ڣ�2���������£�ֱ��д��������POD�ס�NOB�ĵ�P���꣮

���𰸡���1��y=x2+3x����2����m=��2ʱ��S��BOD�����ֵ�����ֵΪ8����ʱD������Ϊ����2����2������3��P������Ϊ��![]() ����
����![]() ����
����![]() ��
��![]() ����
����
��������
�����������ô���ϵ�����Ϳ���������ߵĽ���ʽ��
��D����DC��y�ύOB��C�������D��m��m2+3m������4��m��0������C��m����m���������������������ʽ���㻯��S��BOD=��2��m+2��2+8����������.
��BK��y����K��BI��x����I��BN��y����M�㣬���ı���BIOKΪ�����Σ�������ȫ�������ж������ó�Rt��BIA��Rt��BKM���г�������![]() �����ã�2���������������ۼ������.
�����ã�2���������������ۼ������.
�⣺��1���������߶Գ���Ϊֱ��x=![]() ��
��
��A����3��0����
�������߽���ʽΪy=ax��x+3����
��B����4��4�������a����4������4+3��=4�����a=1��
�������߽���ʽΪy=x��x+3������y=x2+3x��
��2����D����DC��y�ύOB��C����ͼ1��
ֱ��OB�Ľ���ʽΪy=��x��
��D��m��m2+3m������4��m��0������C��m����m����
��DC=��m����m2+3m��=��m2��4m��
��S��BOD=S��BCD+S��OCD=![]() 4DC=��2m2��8m=��2��m+2��2+8��
4DC=��2m2��8m=��2��m+2��2+8��
��m=��2ʱ��S��BOD�����ֵ�����ֵΪ8����ʱD������Ϊ����2����2����
��3����BK��y����K��BI��x����I��BN��y����M�㣬��ͼ2��
���ı���BIOKΪ��������
�ߡ�NBO=��ABO��
���IBA=��KBM��
��BI=KM��
��Rt��BIA��Rt��BKM��
��KM=AI=1��
��M��0��3����
��ֱ��BN�Ľ���ʽΪy=px+q��
��B����4��4����M��0��3�������![]() �����
�����![]() ��
��
��ֱ��BN�Ľ���ʽΪy=��![]() x+3��
x+3��
�ⷽ���� ��
��![]() ��
��![]() ��
��
��N��![]() ��
��![]() ����
����
��OB=4![]() ��OD=2
��OD=2![]() ��
��
��![]() =
=![]() ��
��
���POD����NOB�����Ʊ�Ϊ1��2��
��OB���е�E��EF��BN��ON��F����ͼ2��
���FOE�ס�NOB�����ǵ����Ʊ�Ϊ1��2��
��F��ΪON���е㣬
��F��![]() ��
��![]() ����
����
�ߵ�E���D����x��Գƣ�
���P�����F����x��Գ�ʱ����P��OD�ա�FOE������P��OD�ס�NOB����ʱP�䣨![]() ����
����![]() ����
����
��P�������OD�ĶԳƵ�P��������P��OD�ա�P��OD������P��OD�ס�NOB����ʱP�壨��![]() ��
��![]() ����
����
��������������������P��������![]() ����
����![]() ����
����![]() ��
��![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB��BC����B��90������DΪֱ��BC��һ�����㣨����B��C�غϣ�������AD�����߶�AD�Ƶ�D��˳���뷽����ת90���õ��߶�DE������EC��
��1����ͼ1����D���߶�BC�ϣ������⻭ͼ�õ�ͼ2��
����֤����BAD����EDC��
�ڷ���ͬѧͨ���۲졢�����ó����ۣ��ڵ�D�˶��Ĺ����У����С�DCE��135������������Ҫ˼·�����¼�����
˼·һ����AB��ȡһ��Fʹ��BF��BD��Ҫ֤��DCE��135����ֻ��֤��ADF�ա�DEC��
˼·�����Ե�DΪԲ�ģ�DCΪ�뾶������AC�ڵ�F��Ҫ֤��DCE��135����ֻ��֤��AFD�ա�ECD��
˼·��������E��BC����ֱ�ߵĴ��߶�EF��Ҫ֤��DCE��135����ֻ��֤EF��CF��
����
����ο���ѡ������һ��˼·��֤����DCE��135����
��2�������D���߶�CB���ӳ������˶�������ͼ3��ͼ��������DCE�Ķ�������ȷ����ֵ������ǣ���д����DCE�Ķ�����˵�����ɣ�������ǣ�Ҳ��˵��������ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�����߷ֱ�Ϊ![]() �������������Ƴ���ABC��ֱ�������ε��У� ��
�������������Ƴ���ABC��ֱ�������ε��У� ��
��![]() ;��
;��![]() ;�� ��A����B
;�� ��A����B![]() ��C; �ܡ�A�á�B�á�C��1��2��3 ;��
��C; �ܡ�A�á�B�á�C��1��2��3 ;��![]() ;��
;��![]()
![]()
![]()
A.2��B.3��C.4��D.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��DA��DB��DC�Ǵӵ�D�����������߶Σ���DA=DB=DC��

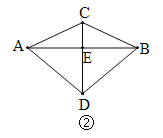
��1����ͼ��������D���߶�![]() �ϣ�����
�ϣ�����![]() �����ж�
�����ж�![]() ����״����˵�����ɣ�
����״����˵�����ɣ�
��2����ͼ�ڣ�����![]() ����
����![]() ��
��![]() �ཻ�ڵ�E����
�ཻ�ڵ�E����![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=ax2+bx+cͼ���һ���֣�ͼ�����A����3��0�����Գ���Ϊֱ��x=��1��
��c��0����2a��b=0����![]() ��0��������B����
��0��������B����![]() ��y1����C����
��y1����C����![]() ��y2��Ϊ����ͼ���ϵ����㣬��y1��y2���ĸ���������ȷ����_____��
��y2��Ϊ����ͼ���ϵ����㣬��y1��y2���ĸ���������ȷ����_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=��1���������н��ۣ�
��b2=4ac����abc��0����a��c����4a��2b+c��0��������ȷ�ĸ����У� ��

A��1�� B��2�� C��3�� D��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���B����C��AB��8��BC��6����DΪAB���е㣬��P���߶�BC����ÿ��2����λ���ٶ��ɵ�B���C�˶���ͬʱ��Q���߶�CA����ÿ��a����λ���ٶ��ɵ�C���A�˶������˶�ʱ��Ϊt���룩��0��t��3����
��1���ú�t�Ĵ���ʽ��ʾ�߶�PC�ij���
��2������P��Q���˶��ٶ���ȣ�t��1ʱ����BPD����CQP�Ƿ�ȫ�ȣ���˵�����ɣ�
��3������P��Q���˶��ٶȲ���ȣ���BPD����CQPȫ��ʱ����a��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ï�ֻ�ջ��������ǰ�� 30000 Ԫ����һ���ʵƽ������ۣ����ڽ������Ҵ�����ʵ�ʿ����� 8 �۵ļ۸������ʵƣ�������Աȼƻ������ 100 յ�ʵƣ�
�Ÿû�ջʵ�ʹ���ÿյ�ʵƶ���Ԫ��
�Ƹû�ջ�����ڽ��۵Ļ����ϣ�ÿյ�ƼӼ� 30%���������ۣ��û�ջҪ���������� 10000 Ԫ��Ӧ�����ٹ����ʵƶ���յ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��B��D�ֱ���CF��EF�ϣ�CB��ED��CA��EA����C����E������AB��AD��
��1����֤��AB��AD��
��2����֤��BF��DF��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com