
【题目】已知,DA,DB,DC是从点D出发的三条线段,且DA=DB=DC.

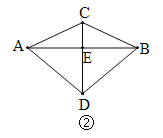
(1)如图①,若点D在线段![]() 上,连结
上,连结![]() .试判断
.试判断![]() 的形状,并说明理由.
的形状,并说明理由.
(2)如图②,连结![]() ,且
,且![]() 与
与![]() 相交于点E.若
相交于点E.若![]() ,
,![]() ,
,![]() ,求
,求![]() 和
和![]() 的长.
的长.
【答案】(1)△ABC是直角三角形;理由见解析;(2)CE=4,AC=![]() .
.
【解析】
(1)根据等边对等角和三角形内角和定理即可得出结论;
(2)用SSS证明△ADC≌△BDC,得出∠ADC=∠BDC,根据等腰三角形三线合一的性质得出DC⊥AB,AE的长.在Rt△ADE中利用勾股定理即可得出DE的长,进而得出CE的长.在Rt△AEC中,根据勾股定理得出AC的长.
(1)△ABC是直角三角形.理由如下:
∵DA=DC,∴∠A=∠ACD.
∵DB=DC,∴∠B=∠BCD.
∵∠A+∠ACD+∠BCD+∠B=180°,
∴∠ACD+∠BCD=∠ACB=90°,
∴△ABC是直角三角形.
(2)∵AD=BD,AC=BC,DC=DC,
∴△ADC≌△BDC,∴∠ADC=∠BDC.
∵AD=BD,∴DC⊥AB,AE=BE=![]() AB=8,
AB=8,
∴DE=![]() =6,
=6,
∴CE=DC-DE=10-6=4,
∴AC=![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,求旗杆的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,AB=BC,∠B=60°,E是BC边上一点.
(1)如图1,若E是BC的中点,∠AED=60°,求证:CE=CD;
(2)如图2,若∠EAD=60°,求证:△AED是等边三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a、b、c是△ABC中∠A、∠B、∠C的对边,抛物线y=x2﹣2ax+b2交x轴于M(a+c,0),则△ABC是( )
A. 等腰三角形 B. 等边三角形 C. 直角三角形 D. 不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6种型号).

根据以上信息,解答下列问题:
(1)该班共有________名学生.
(2)在条形统计图中,请把空缺部分补充完整.
(3)该班学生所穿校服型号的众数为__________型号,中位数为_________型号.
(4)若该校九年级有学生500人,请你估计穿175型号校服的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=ax2+bx+c过原点O和B(﹣4,4),且对称轴为直线x=![]() .
.
(1)求抛物线的函数表达式;
(2)D是直线OB下方抛物线上的一动点,连接OD,BD,在点D运动过程中,当△OBD面积最大时,求点D的坐标和△OBD的最大面积;
(3)如图2,若点P为平面内一点,点N在抛物线上,且∠NBO=∠ABO,则在(2)的条件下,直接写出满足△POD∽△NOB的点P坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线MN分别与直线AC、DG交于点B.F,且∠1=∠2.∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C.

(1)求证:BE∥CF;
(2)若∠C=35°,求∠BED的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
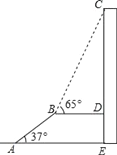
【题目】如图,AB是长为10m,倾斜角为37°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).
(参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin65°≈
,sin65°≈![]() ,tan65°≈
,tan65°≈![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com