
【题目】如图,在四边形ABCD中,AB∥CD,AB=BC,∠B=60°,E是BC边上一点.
(1)如图1,若E是BC的中点,∠AED=60°,求证:CE=CD;
(2)如图2,若∠EAD=60°,求证:△AED是等边三角形.

【答案】(1)见解析;(2)见解析
【解析】
(1)根据AB=BC,∠B=60°得三角形ABC为等边三角形,再根据等边三角形的性质得AE⊥BC,进而证明∠EDC=∠DEC即可;
(2)连接AC,根据两条线平行,同旁内角互补和三角形内角和定理得∠ADC=120°﹣∠BAE,∠AEB=120°﹣∠BAE,即可证明△ABE≌△ACD,进而得结论.
(1)∵AB=BC,∠B=60°,
∴△ABC是等边三角形,
∴∠ACB=60°=∠BAC,
∵E是BC的中点,
∴AE⊥BC,
∴∠AEC=90°,
∵∠AED=60°,
∴∠DEC=30°,
∵AB∥CD,
∴∠ACD=∠BAC=60°,
∴∠ECD=∠ACE+∠ACD=120°,
∴∠CDE=180°﹣120°﹣30°=30°,
∴∠CED=∠CDE,
∴CE=CD.
(2)如图:连接AC,

∵AB=BC,∠B=60°,
∴△ABC是等边三角形,
∴AB=AC,
∵AB∥CD,
∴∠BAD+∠ADC=180°,
∵∠EAD=60°,
∴∠ADC=180°﹣∠EAD﹣∠EAB=120°﹣∠EAB.
在△ABE中,∠AEB=180°﹣∠B﹣∠EAB=120°﹣∠EAB,
∴∠AEB=∠ADC,
∵∠BAE+∠EAC=∠DAC+∠EAC=60°,
∴∠BAE=∠DAC,
∴△ABE≌△ACD(AAS),
∴AE=AD,
∠EAD=60°,
∴△AED是等边三角形.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】如图,坡AB的坡比为1:2.4,坡长AB=130米,坡AB的高为BT.在坡AB的正面有一栋建筑物CH,点H、A、T在同一条地平线MN上.

(1)试问坡AB的高BT为多少米?
(2)若某人在坡AB的坡脚A处和中点D处,观测到建筑物顶部C处的仰角分别为60°和30°,试求建筑物的高度CH.(精确到米, ![]() ≈1.73,
≈1.73, ![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,∠B=90°,点D为直线BC上一个动点(不与B,C重合),连结AD.将线段AD绕点D按顺吋针方向旋转90°得到线段DE,连结EC.
(1)如图1,点D在线段BC上,依题意画图得到图2.
①求证:∠BAD=∠EDC;
②方方同学通过观察、测量得出结论:在点D运动的过程中,总有∠DCE=135°.方方的主要思路有以下几个:
思路一:在AB上取一点F使得BF=BD,要证∠DCE=135°,只需证△ADF≌△DEC.
思路二:以点D为圆心,DC为半径画弧交AC于点F,要证∠DCE=135°,只需证△AFD≌△ECD.
思路三:过点E作BC所在直线的垂线段EF,要证∠DCE=135°,只需证EF=CF.
……
请你参考井选择其中一个思路,证明∠DCE=135°;
(2)如果点D在线段CB的延长线上运动,利用图3画图分析,∠DCE的度数还是确定的值吗?如果是,请写出∠DCE的度数并说明理由;如果不是,也请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品的成本是![]() 元,试销阶段每件商品的售价
元,试销阶段每件商品的售价![]() (元)与产品的销售量
(元)与产品的销售量![]() (件)满足当
(件)满足当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,且
,且![]() 是
是![]() 的一次函数,为了获得最大利润
的一次函数,为了获得最大利润![]() (元),每件产品的销售价应定为( )
(元),每件产品的销售价应定为( )
A. 160元 B. 180元 C. 140元 D. 200元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象经过点
的图象经过点![]() ,对称轴为直线
,对称轴为直线![]() ,一次函数
,一次函数![]() 的图象经过点
的图象经过点![]() ,交
,交![]() 轴于点
轴于点![]() ,交抛物线于另一点
,交抛物线于另一点![]() ,点
,点![]() 、
、![]() 位于点
位于点![]() 的同侧.
的同侧.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 若
若![]() ,求一次函数的解析式;
,求一次函数的解析式;
![]() 在
在![]() 的条件下,当
的条件下,当![]() 时,抛物线的对称轴上是否存在点
时,抛物线的对称轴上是否存在点![]() ,使得
,使得![]() 同时与
同时与![]() 轴和直线
轴和直线![]() 都相切,如果存在,请求出点
都相切,如果存在,请求出点![]() 的坐标,如果不存在,请说明理由.
的坐标,如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC的三边分别为![]() ,下列条件能推出△ABC是直角三角形的有( )
,下列条件能推出△ABC是直角三角形的有( )
①![]() ;②
;②![]() ;③ ∠A=∠B
;③ ∠A=∠B![]() ∠C; ④∠A∶∠B∶∠C=1∶2∶3 ;⑤
∠C; ④∠A∶∠B∶∠C=1∶2∶3 ;⑤![]() ;⑥
;⑥![]()
![]()
![]()
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,DA,DB,DC是从点D出发的三条线段,且DA=DB=DC.

(1)如图①,若点D在线段![]() 上,连结
上,连结![]() .试判断
.试判断![]() 的形状,并说明理由.
的形状,并说明理由.
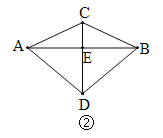
(2)如图②,连结![]() ,且
,且![]() 与
与![]() 相交于点E.若
相交于点E.若![]() ,
,![]() ,
,![]() ,求
,求![]() 和
和![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】茂林货栈打算在年前用 30000 元购进一批彩灯进行销售,由于进货厂家促销,实际可以以 8 折的价格购进这批彩灯,结果可以比计划多购进了 100 盏彩灯.
⑴该货栈实际购进每盏彩灯多少元?
⑵该货栈打算在进价的基础上,每盏灯加价 30%,进行销售,该货栈要想获得利润不低于 10000 元,应至少再购进彩灯多少盏?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com