
【题目】如图,坡AB的坡比为1:2.4,坡长AB=130米,坡AB的高为BT.在坡AB的正面有一栋建筑物CH,点H、A、T在同一条地平线MN上.

(1)试问坡AB的高BT为多少米?
(2)若某人在坡AB的坡脚A处和中点D处,观测到建筑物顶部C处的仰角分别为60°和30°,试求建筑物的高度CH.(精确到米, ![]() ≈1.73,
≈1.73, ![]() ≈1.41)
≈1.41)
【答案】(1)坡AB的高BT为50米;(2)建筑物高度为89米
【解析】试题分析:(1)根据坡AB的坡比为1:2.4,可得tan∠BAT=![]() ,可设TB=h,则AT=2.4h,由勾股定理可得
,可设TB=h,则AT=2.4h,由勾股定理可得![]() ,即可求解,(2) 作DK⊥MN于K,作DL⊥CH于L, 在△ADK中,AD=
,即可求解,(2) 作DK⊥MN于K,作DL⊥CH于L, 在△ADK中,AD=![]() AB=65,KD=
AB=65,KD=![]() BT=25,得AK=60,在△DCL中,∠CDL=30°,令CL=x,得LD=
BT=25,得AK=60,在△DCL中,∠CDL=30°,令CL=x,得LD= ![]() , 易知四边形DLHK是矩形,则LH=DK,LD=HK,在△ACH中,∠CAH=60°,CH=x+25,得AH=
, 易知四边形DLHK是矩形,则LH=DK,LD=HK,在△ACH中,∠CAH=60°,CH=x+25,得AH=![]() , 所以
, 所以![]() ,解得
,解得![]() ,则CH=
,则CH=![]() .
.
试题解析:(1)在△ABT中,∠ATB=90°,BT:AT=1:2.4,AB=130,
令TB=h,则AT=2.4h,
有![]() ,
,
解得h=50(舍负).
答:坡AB的高BT为50米.
(2)作DK⊥MN于K,作DL⊥CH于L,
在△ADK中,AD=![]() AB=65,KD=
AB=65,KD=![]() BT=25,得AK=60,
BT=25,得AK=60,
在△DCL中,∠CDL=30°,令CL=x,得LD= ![]() ,
,
易知四边形DLHK是矩形,则LH=DK,LD=HK,
在△ACH中,∠CAH=60°,CH=x+25,得AH=![]() ,
,
所以![]() ,解得
,解得![]() ,
,
则CH=![]() .
.
答:建筑物高度为89米.


科目:初中数学 来源: 题型:
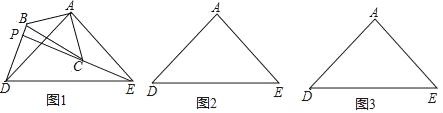
【题目】如图所示,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,EC的延长线交BD于点P.
(1)把△ABC绕点A旋转到图1,BD,CE的关系是 (选填“相等”或“不相等”);简要说明理由;
(2)若AB=3,AD=5,把△ABC绕点A旋转,当∠EAC=90°时,在图2中作出旋转后的图形,PD= ,简要说明计算过程;
(3)在(2)的条件下写出旋转过程中线段PD的最小值为 ,最大值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B在x轴的正半轴上.∠OAB=90°且OA=AB,OB,OC的长分别是二元一次方程组![]() 的解(OB>OC).
的解(OB>OC).

(1)求点A和点B的坐标;
(2)点P是线段OB上的一个动点(点P不与点O,B重合),过点P的直线l与y轴平行,直线l交边OA或边AB于点Q,交边OC或边BC于点R.设点P的横坐标为t,线段QR的长度为m.已知t=4时,直线l恰好过点C.
①当0<t<3时,求m关于t的函数关系式;
②当m=![]() 时,求点P的横坐标t的值.
时,求点P的横坐标t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
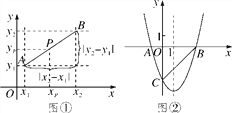
【题目】阅读材料:如图①,在平面直角坐标系中,A,B两点的坐标分别为A(x1,y1),B(x2,y2),AB的中点P的坐标为(xp,yp).由xp-x1=x2-xp,得xp=![]() ,同理得yp=
,同理得yp=![]() ,所以AB的中点坐标为P(
,所以AB的中点坐标为P(![]() ,
,![]() ).由勾股定理得AB2=|x2-x1|2+|y2-y1|2,所以A,B两点间的距离公式为AB=
).由勾股定理得AB2=|x2-x1|2+|y2-y1|2,所以A,B两点间的距离公式为AB=![]() .
.
注:上述公式对A,B在平面直角坐标系中其他位置也成立.
解答下列问题:
如图②,抛物线y=ax2+bx-3(a≠0)与x轴交于A,B两点,与y轴交于点C,且BO=OC=3AO,连接BC.
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,试求出符合条件的P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)直接写出点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE,求P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场第1次用39万元购进A、B两种商品,销售完后获得利润6万元,它们的进价和售价如下表:(总利润=单件利润×销售量)

(1)该商场第1次购进A、B两种商品各多少件?
(2)商场第2次以原价购进A、B两种商品,购进A商品的件数不变,而购进B商品的件数是第1次的2倍,A商品按原价销售,而B商品打折销售,若两种商品销售完毕,要使得第2次经营活动获得利润等于54000元,则B种商品是打几折销售的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中小学时期是学生身心变化最为明显的时期,这个时期孩子们的身高变化呈现一定的趋势,7~15岁期间生子们会经历一个身高发育较迅速的阶段,我们把这个年龄阶段叫做生长速度峰值段,小明通过上网查阅《2016年某市儿童体格发育调查表》,了解某市男女生7~15岁身高平均值记录情况,并绘制了如下统计图,并得出以下结论:
①10岁之前,同龄的女生的平均身高一般会略高于男生的平均身高;
②10~12岁之间,女生达到生长速度峰值段,身高可能超过同龄男生;
③7~15岁期间,男生的平均身高始终高于女生的平均身高;
④13~15岁男生身高出现生长速度峰值段,男女生身高差距可能逐渐加大.
以上结论正确的是( )
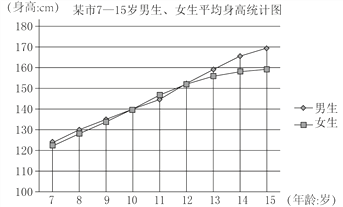
A. ①③ B. ②③ C. ②④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
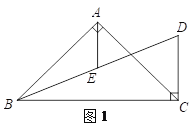
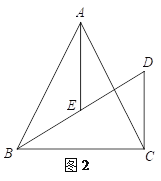
【题目】在△ABC中,AB=AC,CD⊥BC于点C,交∠ABC的平分线于点D,AE平分∠BAC交BD于点E,过点E作EF∥BC交AC于点F,连接DF.
(1)补全图1;
(2)如图1,当∠BAC=90°时,
①求证:BE=DE;
②写出判断DF与AB的位置关系的思路(不用写出证明过程);
(3)如图2,当∠BAC=α时,直接写出α,DF,AE的关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com