
【题目】如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B在x轴的正半轴上.∠OAB=90°且OA=AB,OB,OC的长分别是二元一次方程组![]() 的解(OB>OC).
的解(OB>OC).

(1)求点A和点B的坐标;
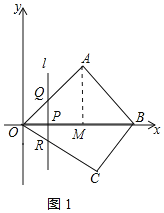
(2)点P是线段OB上的一个动点(点P不与点O,B重合),过点P的直线l与y轴平行,直线l交边OA或边AB于点Q,交边OC或边BC于点R.设点P的横坐标为t,线段QR的长度为m.已知t=4时,直线l恰好过点C.
①当0<t<3时,求m关于t的函数关系式;
②当m=![]() 时,求点P的横坐标t的值.
时,求点P的横坐标t的值.
【答案】(1)点B的坐标为:(6,0),点A的坐标为:(3,3);(2)①m=![]() t;②满足条件的点P的横坐标t的值为2或
t;②满足条件的点P的横坐标t的值为2或![]() .
.
【解析】
(1)求出方程![]() 的解为
的解为![]() ,得出OB=6,OC=5,点B的坐标为:(6,0),过点作AM⊥轴于M,则△AOB是等直角三角形,得出OM=BM=AM=
,得出OB=6,OC=5,点B的坐标为:(6,0),过点作AM⊥轴于M,则△AOB是等直角三角形,得出OM=BM=AM=![]() OB=3,即可得出答;
OB=3,即可得出答;
(2)①过点C作CN⊥x轴于N,由题意得出ON=4,由勾股定理得出CN=![]() =3,得出点C的坐标为:(4,-3),由待定系数法求出直线OC的解析式为:y=
=3,得出点C的坐标为:(4,-3),由待定系数法求出直线OC的解析式为:y=![]() x,得出R(t,
x,得出R(t,![]() t),由待定系数法直线OA的解析式为:y=x,得出Q(t,t),即可得出结果;
t),由待定系数法直线OA的解析式为:y=x,得出Q(t,t),即可得出结果;
②分三种情况:当![]() 时,m=
时,m=![]() , m=
, m=![]() , 则t=2;
, 则t=2;
当3≤t<14时,由得定系数法出直AB的解析式为![]() 得出Q(
得出Q(![]() ),R
),R![]() )得出方程
)得出方程![]() 解方程即可;
解方程即可;
当4≤t<6时,由待定系数法求出直线BC的解析式为:y=![]() x-9,得Q(t,-t+6),R(t,
x-9,得Q(t,-t+6),R(t,![]() t-9),得出方程,解方程即可.
t-9),得出方程,解方程即可.
解:(1)方程组![]() 的解为:
的解为:![]() ,
,
∵OB>OC,
∴OB=6,OC=5,
∴点B的坐标为:(6,0),
过点A作AM⊥x轴于M,如图1所示:
∵∠OAB=90°且OA=AB,
∴△AOB是等腰直角三角形,
∴OM=BM=AM=![]() OB=
OB=![]() ×6=3,
×6=3,
∴点A的坐标为:(3,3);
(2)①过点C作CN⊥x轴于N,如图2所示:
∵t=4时,直线l恰好过点C,
∴ON=4,
CN=![]() =
=![]() =3,
=3,
∴点C的坐标为:(4,﹣3),
设直线OC的解析式为:y=kx,
把C(4,﹣3)代入得:﹣3=4k,
∴k=﹣![]() ,
,
∴直线OC的解析式为:y=﹣![]() x,
x,
∴R(t,﹣![]() t),
t),
设直线OA的解析式为:y=k′x,
把A(3,3)代入得:3=3k′,
∴k′=1,
∴直线OA的解析式为:y=x,
∴Q(t,t),
∴QR=t﹣(﹣![]() t)=
t)=![]() t,
t,
即:m=![]() t;
t;
②分三种情况:
当0<t<3时,m=![]() t,m=
t,m=![]() ,
,
则![]() t=
t=![]() ,
,
解得:t=2;
当3≤t<4时,设直线AB的解析式为:y=px+q,
把A(3,3)、B(6,0)代入得![]() ,
,
解得:![]() ,
,
∴直线AB的解析式为:y=﹣x+6,
∴Q(t,﹣t+6),R(t,﹣![]() t),
t),
∴m=﹣t+6﹣(﹣![]() t)=﹣
t)=﹣![]() t+6,
t+6,
∵m=![]() ,
,
∴﹣![]() t+6=
t+6=![]() ,
,
解得:t=10>6(不合题意舍去);
当4≤t<6时,设直线BC的解析式为:y=ax+b,
把B(6,0)、C(4,﹣3)代入得![]() ,
,
解得: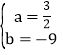 ,
,
∴直线BC的解析式为:y=![]() x﹣9,
x﹣9,
∴Q(t,﹣t+6),R(t,![]() t﹣9),
t﹣9),
∴m=﹣t+6﹣(![]() t﹣9)=﹣
t﹣9)=﹣![]() t+15,
t+15,
∵m=![]() ,
,
∴﹣![]() t+15=
t+15=![]() ,
,
解得:t=![]() ;
;
综上所述,满足条件的点P的横坐标t的值为2或![]() .
.


科目:初中数学 来源: 题型:
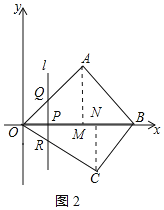
【题目】如图,已知二次函数y=﹣x2+bx+c(c>0)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=OC=3,顶点为M.
(1)求二次函数的解析式;
(2)点P为线段BM上的一个动点,过点P作x轴的垂线PQ,垂足为Q,若OQ=m,四边形ACPQ的面积为S,求S关于m的函数解析式,并写出m的取值范围;
(3)探索:线段BM上是否存在点N,使△NMC为等腰三角形?如果存在,求出点N的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
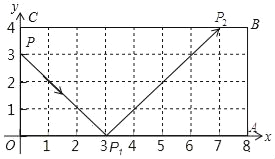
【题目】如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时,记为点P1,第2次碰到矩形的边时,记为点P2,…第n次碰到矩形的边时,记为点Pn,则点P4的坐标是_____;点P125的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司开发了一种新产品,现要在甲地或者乙地进行销售,设年销售量为x(件),其中x>0.
若在甲地销售,每件售价y(元)与x之间的函数关系式为y=﹣![]() x+100,每件成本为20元,设此时的年销售利润为w甲(元)(利润=销售额﹣成本).
x+100,每件成本为20元,设此时的年销售利润为w甲(元)(利润=销售额﹣成本).
若在乙地销售,受各种不确定因素的影响,每件成本为a元(a为常数,18≤a≤25 ),每件售价为98元,销售x(件)每年还需缴纳![]() x2元的附加费.设此时的年销售利润为w乙(元)(利润=销售额﹣成本﹣附加费).
x2元的附加费.设此时的年销售利润为w乙(元)(利润=销售额﹣成本﹣附加费).
(1)当a=18,且x=100是,w乙= 元;
(2)求w甲与x之间的函数关系式(不必写出x的取值范围),当w甲=15000时,若使销售量最大,求x的值;
(3)为完成x件的年销售任务,请你通过分析帮助公司决策,应选择在甲地还是在乙地销售才能使该公司所获年利润最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有三点A、B、C,请根据图回答下列问题:
![]()
(1)若将点B向左平移3个单位后,则A、B、C这三个点所表示的数谁最小?是多少?
(2)若将点A向右平移4个单位后,则A、B、C这三个点所表示的数谁最大?最大的数比最小的数大多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
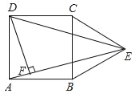
【题目】如图,在正方形ABCD的外侧,作等边三角形BCE,连接AE,DE.
(1)求证:AE=DE
(2)过点D作DF⊥AE,垂足为F,若AB=2cm,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,坡AB的坡比为1:2.4,坡长AB=130米,坡AB的高为BT.在坡AB的正面有一栋建筑物CH,点H、A、T在同一条地平线MN上.

(1)试问坡AB的高BT为多少米?
(2)若某人在坡AB的坡脚A处和中点D处,观测到建筑物顶部C处的仰角分别为60°和30°,试求建筑物的高度CH.(精确到米, ![]() ≈1.73,
≈1.73, ![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016·长沙中考)若抛物线L:y=ax2+x+c(a,b,c是常数,abc≠0)与直线l都经过y轴上的一点P,且抛物线L的顶点Q在直线l上,则称此直线l与该抛物线L具有“一带一路”关系,此时,直线l叫作抛物线L的“带线”,抛物线L叫作直线l的“路线”.
(1)若直线y=mx+1与抛物线y=x2-2x+n具有“一带一路”关系,求m,n的值;
(2)若某“路线”L的顶点在反比例函数y=![]() 的图象上,它的“带线”l的解析式为y=2x-4,求此“路线”L的解析式.
的图象上,它的“带线”l的解析式为y=2x-4,求此“路线”L的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com