
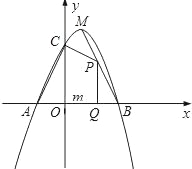
【题目】如图,已知二次函数y=﹣x2+bx+c(c>0)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=OC=3,顶点为M.
(1)求二次函数的解析式;
(2)点P为线段BM上的一个动点,过点P作x轴的垂线PQ,垂足为Q,若OQ=m,四边形ACPQ的面积为S,求S关于m的函数解析式,并写出m的取值范围;
(3)探索:线段BM上是否存在点N,使△NMC为等腰三角形?如果存在,求出点N的坐标;如果不存在,请说明理由.
【答案】(1) 二次函数的解析式为y=﹣x2+2x+3;(2)S=﹣m2+![]() m+
m+![]() (1≤m<3);(3) (
(1≤m<3);(3) (![]() ,
, ![]() )(1+
)(1+![]() ,4﹣
,4﹣![]() )(2,2).
)(2,2).
【解析】解:(1)∵OB=OC=3,
∴B(3,0),C(0,3)
∴![]() ,
,
解得![]() ,
,
∴二次函数的解析式为y=﹣x2+2x+3;
(2)y=﹣x2+2x+3=﹣(x﹣1)2+4,M(1, 4)
设直线MB的解析式为y=kx+n,
则有![]() ,
,
解得![]() ,
,
∴直线MB的解析式为y=﹣2x+6,
∵PQ⊥x轴,OQ=m,
∴点P的坐标为(m,﹣2m+6)
S四边形ACPQ=S△AOC+S梯形PQOC=![]() AOCO+
AOCO+![]() (PQ+CO)OQ(1≤m<3)
(PQ+CO)OQ(1≤m<3)
=![]() ×1×3+
×1×3+![]() (﹣2m+6+3)m=﹣m2+
(﹣2m+6+3)m=﹣m2+![]() m+
m+![]() ;
;
(3)线段BM上存在点N(![]() ,
, ![]() ),(2,2),(1+
),(2,2),(1+![]() ,4﹣
,4﹣![]() )使△NMC为等腰三角形,
)使△NMC为等腰三角形,
CM=![]() ,CN=
,CN=![]() ,MN=
,MN=![]()
①当CM=NC时, ![]() ,
,
解得x1=![]() ,x2=1(舍去)
,x2=1(舍去)
此时N(![]() ,
, ![]() ),
),
②当CM=MN时, ![]() ,
,
解得x1=1+![]() ,x2=1-
,x2=1-![]() 舍去),
舍去),
此时N(1+![]() ,4﹣
,4﹣![]() ).
).
③当CN=MN时, ![]() ,
,
解得x=2,此时N(2,2).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | …… |
月销量(件) | 200 | 180 | 160 | 140 | …… |
(1)已知该运动服的进价为每件60元,设售价为x元;
请用含有x的式子表示:
①销售该运动服每件的利润是 元;
②月销售量是 件;(直接写结果)
(2)设销售该运动服的月利润为y元,那么售价为多少元时,当月的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点A(2,0)的两条直线![]() ,
,![]() 分别交
分别交![]() 轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=
轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=![]() .
.

(1)求点B的坐标;
(2)若△ABC的面积为4,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图a是长方形纸带,∠DEF=24°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图 c中的∠CFE的度数是( )

A.104°B.106°C.108°D.110°
查看答案和解析>>
科目:初中数学 来源: 题型:
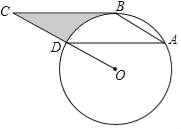
【题目】如图所示,点ABD都在⊙O上,BC是⊙O的切线,AD∥BC,∠C=30°,AD=4![]() .
.
(1)求∠A的度数;
(2)求由线段BC、CD与弧BD所围成的阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在11月11日这一天,上午卖出某品牌手机75部,下午又卖出100部,已知每部手机的售价为a元,每部手机的成本为b元.
(1)求这一天该公司卖出该品牌手机的总销售额.
(2)求这一天该公司卖出该品牌手机所得的利润.
(3)当a=6800,b=2700时,总销售额和利润分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a,b互为相反数,c,d互为倒数,m的绝对值是1,n是有理数且既不是正数也不是负数,求20161﹣(a+b)+m![]() ﹣(cd)2016+n(a+b+c+d)的值.
﹣(cd)2016+n(a+b+c+d)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
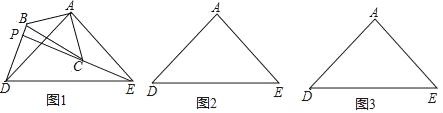
【题目】如图所示,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,EC的延长线交BD于点P.
(1)把△ABC绕点A旋转到图1,BD,CE的关系是 (选填“相等”或“不相等”);简要说明理由;
(2)若AB=3,AD=5,把△ABC绕点A旋转,当∠EAC=90°时,在图2中作出旋转后的图形,PD= ,简要说明计算过程;
(3)在(2)的条件下写出旋转过程中线段PD的最小值为 ,最大值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B在x轴的正半轴上.∠OAB=90°且OA=AB,OB,OC的长分别是二元一次方程组![]() 的解(OB>OC).
的解(OB>OC).

(1)求点A和点B的坐标;
(2)点P是线段OB上的一个动点(点P不与点O,B重合),过点P的直线l与y轴平行,直线l交边OA或边AB于点Q,交边OC或边BC于点R.设点P的横坐标为t,线段QR的长度为m.已知t=4时,直线l恰好过点C.
①当0<t<3时,求m关于t的函数关系式;
②当m=![]() 时,求点P的横坐标t的值.
时,求点P的横坐标t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com