
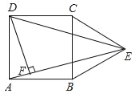
【题目】如图,在正方形ABCD的外侧,作等边三角形BCE,连接AE,DE.
(1)求证:AE=DE
(2)过点D作DF⊥AE,垂足为F,若AB=2cm,求DF的长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)证明△ABE≌△DCE,可得结论;
(2)作辅助线,构建直角三角形,根据等腰三角形的性质得∠BCG=30°,∠DEF=30°,利用正方形的边长计算DE的长,从而得DF的长.
(1)证明:∵四边形ABCD是正方形,
∴AB=CD,∠ABC=∠DCB=90°,
∵△BCE是等边三角形,
∴BE=CE,∠EBC=∠ECB=60°,
即∠ABE=∠DCE=150°,
∴△ABE≌△DCE,
∴AE=DE;
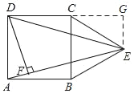
(2)解:过点E作EG⊥CD于G,
∵DC=CE,∠DCE=150°,
∴∠CDE=∠CED=15°,
∴∠ECG=30°,
∵CB=CD=AB=2,
∴EG=1,CG=![]() ,
,
在Rt△DGE中,DE=![]() ,
,
在Rt△DEF中,∠EDA=∠DAE=90°﹣15°=75°
∴∠DEF=30°,
∴DF=![]() DE=
DE=![]() (cm).
(cm).


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】若a,b互为相反数,c,d互为倒数,m的绝对值是1,n是有理数且既不是正数也不是负数,求20161﹣(a+b)+m![]() ﹣(cd)2016+n(a+b+c+d)的值.
﹣(cd)2016+n(a+b+c+d)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型商业中心开业,为吸引顾客,特在一指定区域放置一批按摩休闲椅,供顾客有偿体验,收费如下图:
(1)若在此按摩椅上连续休息了1小时,需要支付多少元?
(2)某人在该椅上一次性消费18元,那么他在该椅子上最多休息了多久?
(3)张先生到该商场会见一名客人,结果客人告知临时有事,预计4.5小时后才能到来;那么如果张先生要在该休闲椅上休息直至客人到来,他至少需要支付多少钱?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B在x轴的正半轴上.∠OAB=90°且OA=AB,OB,OC的长分别是二元一次方程组![]() 的解(OB>OC).
的解(OB>OC).

(1)求点A和点B的坐标;
(2)点P是线段OB上的一个动点(点P不与点O,B重合),过点P的直线l与y轴平行,直线l交边OA或边AB于点Q,交边OC或边BC于点R.设点P的横坐标为t,线段QR的长度为m.已知t=4时,直线l恰好过点C.
①当0<t<3时,求m关于t的函数关系式;
②当m=![]() 时,求点P的横坐标t的值.
时,求点P的横坐标t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张先生今年7月份第一个星期的星期五以每股(份)25元的价格买进某种金融理财产品共2000股(买入时免收手续费),该理财产品在第二个星期的五个交易日中,每股的涨跌情况如下表(表格中数据表示比前一交易日涨或跌多少元) (单位:元):
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌额 |
|
|
|
|
|
(1)写出第二个星期每日每股理财产品的收盘价(即每日最后时刻的成交价);
(2)已知理财产品卖出时,交易所需收取千分之三的手续费,如果张先生在第二个星期的星期五交易结束前将全部产品卖出,他的收益情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
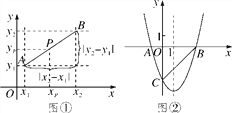
【题目】阅读材料:如图①,在平面直角坐标系中,A,B两点的坐标分别为A(x1,y1),B(x2,y2),AB的中点P的坐标为(xp,yp).由xp-x1=x2-xp,得xp=![]() ,同理得yp=
,同理得yp=![]() ,所以AB的中点坐标为P(
,所以AB的中点坐标为P(![]() ,
,![]() ).由勾股定理得AB2=|x2-x1|2+|y2-y1|2,所以A,B两点间的距离公式为AB=
).由勾股定理得AB2=|x2-x1|2+|y2-y1|2,所以A,B两点间的距离公式为AB=![]() .
.
注:上述公式对A,B在平面直角坐标系中其他位置也成立.
解答下列问题:
如图②,抛物线y=ax2+bx-3(a≠0)与x轴交于A,B两点,与y轴交于点C,且BO=OC=3AO,连接BC.
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,试求出符合条件的P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)直接写出点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE,求P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数的图象经过点A(2,1),B(﹣1,﹣3).
(1)求此一次函数的解析式;
(2)求此一次函数的图象与x轴、y轴的交点坐标;
(3)求此一次函数的图象与两坐标轴所围成的三角形面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com