
【题目】(2016·长沙中考)若抛物线L:y=ax2+x+c(a,b,c是常数,abc≠0)与直线l都经过y轴上的一点P,且抛物线L的顶点Q在直线l上,则称此直线l与该抛物线L具有“一带一路”关系,此时,直线l叫作抛物线L的“带线”,抛物线L叫作直线l的“路线”.
(1)若直线y=mx+1与抛物线y=x2-2x+n具有“一带一路”关系,求m,n的值;
(2)若某“路线”L的顶点在反比例函数y=![]() 的图象上,它的“带线”l的解析式为y=2x-4,求此“路线”L的解析式.
的图象上,它的“带线”l的解析式为y=2x-4,求此“路线”L的解析式.
【答案】(1)m=-1,n=1;(2)y=2(x+1)2-6或y=-![]() (x-3)2+2.
(x-3)2+2.
【解析】试题分析: (1)令直线y=mx+1中x=0,则y=1,所以该直线与y轴的交点为(0,1),将(0,1)代入抛物线y=x2-2x+n中,得n=1,可求出抛物线的解析式为y=x2-2x+1=(x-1)2,所以抛物线的顶点坐标为(1,0).将点(1,0)代入到直线y=mx+1中,得0=m+1,解得m=-1,
(2)将y=2x-4和y=![]() 联立方程可得2x-4=
联立方程可得2x-4=![]() ,即2x2-4x-6=0,解得x1=-1,x2=3,所以该“路线”L的顶点坐标为(-1,-6)或(3,2),令“带线”l:y=2x-4中x=0,则y=-4,所以 “路线”L的图象过点(0,-4),设该“路线”L的解析式为y=m(x+1)2-6或y=n(x-3)2+2,由题意得:-4=m(0+1)2-6或-4=n(0-3)2+2,解得m=2,n=
,即2x2-4x-6=0,解得x1=-1,x2=3,所以该“路线”L的顶点坐标为(-1,-6)或(3,2),令“带线”l:y=2x-4中x=0,则y=-4,所以 “路线”L的图象过点(0,-4),设该“路线”L的解析式为y=m(x+1)2-6或y=n(x-3)2+2,由题意得:-4=m(0+1)2-6或-4=n(0-3)2+2,解得m=2,n=![]() ,所以此“路线”L的解析式为y=2(x+1)2-6或y=
,所以此“路线”L的解析式为y=2(x+1)2-6或y=![]() (x-3)2+2.
(x-3)2+2.
试题解析:(1)令直线y=mx+1中x=0,则y=1,即该直线与y轴的交点为(0,1),将(0,1)代入抛物线y=x2-2x+n中,得n=1,
∴抛物线的解析式为y=x2-2x+1=(x-1)2,
∴抛物线的顶点坐标为(1,0).将点(1,0)代入到直线y=mx+1中,得0=m+1,解得m=-1,
(2)将y=2x-4代入到y=![]() 中,得2x-4=
中,得2x-4=![]() ,即2x2-4x-6=0,解得x1=-1,x2=3,
,即2x2-4x-6=0,解得x1=-1,x2=3,
∴该“路线”L的顶点坐标为(-1,-6)或(3,2),
令“带线”l:y=2x-4中x=0,则y=-4,
∴“路线”L的图象过点(0,-4),
设该“路线”L的解析式为y=m(x+1)2-6或y=n(x-3)2+2,由题意得:
-4=m(0+1)2-6或-4=n(0-3)2+2,解得m=2,n=![]() ,
,
∴此“路线”L的解析式为y=2(x+1)2-6或y=![]() (x-3)2+2.
(x-3)2+2.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B在x轴的正半轴上.∠OAB=90°且OA=AB,OB,OC的长分别是二元一次方程组![]() 的解(OB>OC).
的解(OB>OC).

(1)求点A和点B的坐标;
(2)点P是线段OB上的一个动点(点P不与点O,B重合),过点P的直线l与y轴平行,直线l交边OA或边AB于点Q,交边OC或边BC于点R.设点P的横坐标为t,线段QR的长度为m.已知t=4时,直线l恰好过点C.
①当0<t<3时,求m关于t的函数关系式;
②当m=![]() 时,求点P的横坐标t的值.
时,求点P的横坐标t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中小学时期是学生身心变化最为明显的时期,这个时期孩子们的身高变化呈现一定的趋势,7~15岁期间生子们会经历一个身高发育较迅速的阶段,我们把这个年龄阶段叫做生长速度峰值段,小明通过上网查阅《2016年某市儿童体格发育调查表》,了解某市男女生7~15岁身高平均值记录情况,并绘制了如下统计图,并得出以下结论:
①10岁之前,同龄的女生的平均身高一般会略高于男生的平均身高;
②10~12岁之间,女生达到生长速度峰值段,身高可能超过同龄男生;
③7~15岁期间,男生的平均身高始终高于女生的平均身高;
④13~15岁男生身高出现生长速度峰值段,男女生身高差距可能逐渐加大.
以上结论正确的是( )
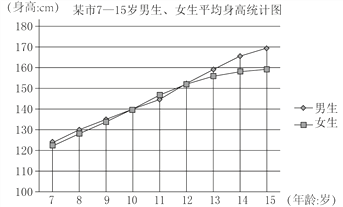
A. ①③ B. ②③ C. ②④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
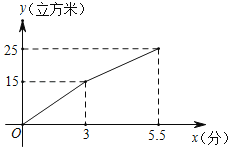
【题目】某种水泥储存罐的容量为25立方米,它有一个输入口和一个输出口.从某时刻开始,只打开输入口,匀速向储存罐内注入水泥,3分钟后,再打开输出口,匀速向运输车输出水泥,又经过2.5分钟储存罐注满,关闭输入口,保持原来的输出速度继续向运输车输出水泥,当输出的水泥总量达到8立方米时,关闭输出口.储存罐内的水泥量y(立方米)与时间x(分)之间的部分函数图象如图所示.
(1)求每分钟向储存罐内注入的水泥量.
(2)当3≤x≤5.5时,求y与x之间的函数关系式.
(3)储存罐每分钟向运输车输出的水泥量是 立方米,从打开输入口到关闭输出口共用的时间为 分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大于1的正整数的三次方都可以分解为若干个连续奇数的和.如23=3+5,33=7+9+11,43=13+15+17+19.按此规律,若m3分解后,最后一个奇数为109,则m的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数的图象经过点A(2,1),B(﹣1,﹣3).
(1)求此一次函数的解析式;
(2)求此一次函数的图象与x轴、y轴的交点坐标;
(3)求此一次函数的图象与两坐标轴所围成的三角形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
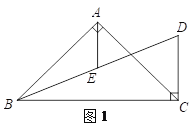
【题目】在△ABC中,AB=AC,CD⊥BC于点C,交∠ABC的平分线于点D,AE平分∠BAC交BD于点E,过点E作EF∥BC交AC于点F,连接DF.
(1)补全图1;
(2)如图1,当∠BAC=90°时,
①求证:BE=DE;
②写出判断DF与AB的位置关系的思路(不用写出证明过程);
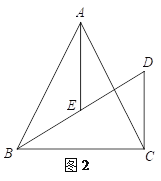
(3)如图2,当∠BAC=α时,直接写出α,DF,AE的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点A在x轴上,点B的坐标为(8,2),点D的坐标为(0,2),则菱形ABCD面积为( )
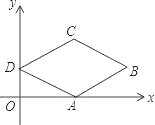
A. 8B. 16C. 24D. 32
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com