
【题目】(1)用配方法解方程:x2﹣2x﹣1=0.
(2)解方程:2x2+3x﹣1=0.
(3)解方程:x2﹣4=3(x+2).
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图a是长方形纸带,∠DEF=24°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图 c中的∠CFE的度数是( )

A.104°B.106°C.108°D.110°
查看答案和解析>>
科目:初中数学 来源: 题型:
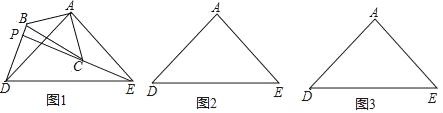
【题目】如图所示,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,EC的延长线交BD于点P.
(1)把△ABC绕点A旋转到图1,BD,CE的关系是 (选填“相等”或“不相等”);简要说明理由;
(2)若AB=3,AD=5,把△ABC绕点A旋转,当∠EAC=90°时,在图2中作出旋转后的图形,PD= ,简要说明计算过程;
(3)在(2)的条件下写出旋转过程中线段PD的最小值为 ,最大值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
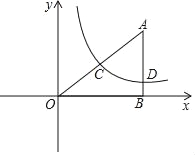
【题目】如图,Rt△ABO在直角坐标系中,AB⊥x轴于点B,AO=10,sin∠AOB=![]() .
.
(1)若反比例函数y=![]() (x>0)的图象经过AO的中点C,求k的值;
(x>0)的图象经过AO的中点C,求k的值;
(2)在(1)的条件下,若反比例函数y=![]() (x>0)的图象与AB交于点D,当点C,D位于直线l:y=﹣x+b的异侧时,求b的取值范围;
(x>0)的图象与AB交于点D,当点C,D位于直线l:y=﹣x+b的异侧时,求b的取值范围;
(3)若点D关于y轴的对称点为E,当反比例函数y=![]() 的图象和线段AE有公共点时,直接写出k的取值范围.
的图象和线段AE有公共点时,直接写出k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型商业中心开业,为吸引顾客,特在一指定区域放置一批按摩休闲椅,供顾客有偿体验,收费如下图:
(1)若在此按摩椅上连续休息了1小时,需要支付多少元?
(2)某人在该椅上一次性消费18元,那么他在该椅子上最多休息了多久?
(3)张先生到该商场会见一名客人,结果客人告知临时有事,预计4.5小时后才能到来;那么如果张先生要在该休闲椅上休息直至客人到来,他至少需要支付多少钱?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店11月份购进甲、乙两种水果共花费1700元,其中甲种水果8元/千克,乙种水果18元/千克.12月份,这两种水果的进价上调为:甲种水果10元/千克,乙种水果20元/千克.
(1)若该店12月份购进这两种水果的数量与11月份都相同,将多支付货款300元,求该店11月份购进甲、乙两种水果分别是多少千克?
(2)若12月份将这两种水果进货总量减少到120千克,设购进甲种水果a千克,需要支付的货款为w元,求w与a的函数关系式;
(3)在(2)的条件下,若甲种水果不超过90千克,则12月份该店需要支付这两种水果的货款最少应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B在x轴的正半轴上.∠OAB=90°且OA=AB,OB,OC的长分别是二元一次方程组![]() 的解(OB>OC).
的解(OB>OC).

(1)求点A和点B的坐标;
(2)点P是线段OB上的一个动点(点P不与点O,B重合),过点P的直线l与y轴平行,直线l交边OA或边AB于点Q,交边OC或边BC于点R.设点P的横坐标为t,线段QR的长度为m.已知t=4时,直线l恰好过点C.
①当0<t<3时,求m关于t的函数关系式;
②当m=![]() 时,求点P的横坐标t的值.
时,求点P的横坐标t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
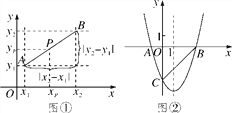
【题目】阅读材料:如图①,在平面直角坐标系中,A,B两点的坐标分别为A(x1,y1),B(x2,y2),AB的中点P的坐标为(xp,yp).由xp-x1=x2-xp,得xp=![]() ,同理得yp=
,同理得yp=![]() ,所以AB的中点坐标为P(
,所以AB的中点坐标为P(![]() ,
,![]() ).由勾股定理得AB2=|x2-x1|2+|y2-y1|2,所以A,B两点间的距离公式为AB=
).由勾股定理得AB2=|x2-x1|2+|y2-y1|2,所以A,B两点间的距离公式为AB=![]() .
.
注:上述公式对A,B在平面直角坐标系中其他位置也成立.
解答下列问题:
如图②,抛物线y=ax2+bx-3(a≠0)与x轴交于A,B两点,与y轴交于点C,且BO=OC=3AO,连接BC.
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,试求出符合条件的P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
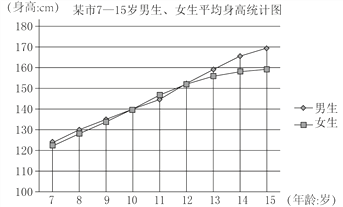
【题目】中小学时期是学生身心变化最为明显的时期,这个时期孩子们的身高变化呈现一定的趋势,7~15岁期间生子们会经历一个身高发育较迅速的阶段,我们把这个年龄阶段叫做生长速度峰值段,小明通过上网查阅《2016年某市儿童体格发育调查表》,了解某市男女生7~15岁身高平均值记录情况,并绘制了如下统计图,并得出以下结论:
①10岁之前,同龄的女生的平均身高一般会略高于男生的平均身高;
②10~12岁之间,女生达到生长速度峰值段,身高可能超过同龄男生;
③7~15岁期间,男生的平均身高始终高于女生的平均身高;
④13~15岁男生身高出现生长速度峰值段,男女生身高差距可能逐渐加大.
以上结论正确的是( )
A. ①③ B. ②③ C. ②④ D. ③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com