
����Ŀ��ij��˾������һ���²�Ʒ����Ҫ�ڼػ����ҵؽ������ۣ�����������Ϊx������������x��0��
���ڼ����ۣ�ÿ���ۼ�y��Ԫ����x֮��ĺ�����ϵʽΪy=��![]() x+100��ÿ���ɱ�Ϊ20Ԫ�����ʱ������������Ϊw����Ԫ��������=���۶�ɱ�����
x+100��ÿ���ɱ�Ϊ20Ԫ�����ʱ������������Ϊw����Ԫ��������=���۶�ɱ�����
�����ҵ����ۣ��ܸ��ֲ�ȷ�����ص�Ӱ�죬ÿ���ɱ�ΪaԪ��aΪ������18��a��25������ÿ���ۼ�Ϊ98Ԫ������x������ÿ�껹�����![]() x2Ԫ�ĸ��ӷѣ����ʱ������������Ϊw����Ԫ��������=���۶�ɱ������ӷѣ���
x2Ԫ�ĸ��ӷѣ����ʱ������������Ϊw����Ԫ��������=���۶�ɱ������ӷѣ���
��1����a=18����x=100�ǣ�w��=�� ��Ԫ��
��2����w����x֮��ĺ�����ϵʽ������д��x��ȡֵ��Χ������w��=15000ʱ����ʹ�����������x��ֵ��
��3��Ϊ���x������������������ͨ������������˾���ߣ�Ӧѡ���ڼػ������ҵ����۲���ʹ�ù�˾�������������
���𰸡���1��7000����2��x=500����3��Ӧѡ���ڼ�����
������������: ��1����������=���۶�-�ɱ�-���ӷѵó�w���ĺ�������ʽΪw��=��98-a��x-![]() x2��������ֵ��ô𰸼��ɣ���2����������=���۶�-�ɱ����w����x֮��ĺ�����ϵʽ�������䷽�������ֵ���ɣ���3���ȼ���õ�w��-w��=��a��18��x����18��a��25����w��-w����0�����űȽ��������������ֵ��Ȼ�����ѡ���ڼػ������ҵأ�
x2��������ֵ��ô𰸼��ɣ���2����������=���۶�-�ɱ����w����x֮��ĺ�����ϵʽ�������䷽�������ֵ���ɣ���3���ȼ���õ�w��-w��=��a��18��x����18��a��25����w��-w����0�����űȽ��������������ֵ��Ȼ�����ѡ���ڼػ������ҵأ�
��⣺��1����a=18����x=100ʱ��w��=��98��18����100��![]() ��1002=7000��Ԫ����
��1002=7000��Ԫ����
�ʴ�Ϊ��7000��
��2��w��=x��y��20��=x����![]() x+100��20��=��
x+100��20��=��![]() x2+80x��
x2+80x��
��w��=15000ʱ����![]() x2+80x=15000��
x2+80x=15000��
��ã�x1=300��x2=500��
����ʹ���������
��x=500��
��3����w��=��![]() x2+��98��a��x��
x2+��98��a��x��
��w����w��=��![]() x2+80x��[��
x2+80x��[��![]() x2+��98��a��x]=��a��18��x��
x2+��98��a��x]=��a��18��x��
��18��a��25����x��0��
��w����w����0����w����w����
��Ӧѡ���ڼ����ۣ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
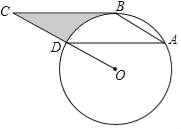
����Ŀ����ͼ��ʾ����ABD������O�ϣ�BC����O�����ߣ�AD��BC����C=30�㣬AD=4![]() ��
��
��1������A�Ķ�����
��2�������߶�BC��CD�뻡BD��Χ�ɵ���Ӱ���ֵ����������������У�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��װ��˾�й�����ŵ����������ÿ�¹�������4000Ԫ��ÿ�칤��8Сʱ��һ���¹���25�죮�¹��ʵ�н1000Ԫ�����ӼƼ����ʣ��ӹ�1��A�ͷ�װ�Ƴ�20Ԫ���ӹ�1��B�ͷ�װ�Ƴ�15Ԫ���ڹ����з���һ���������ӹ�2��A�ͷ�װ��3��B�ͷ�װ��7Сʱ���ӹ�1��A�ͷ�װ��2��B�ͷ�װ��4Сʱ��(�����¹��ʣ���н+�Ƽ�����)
(1)һ���������ӹ�1��A�ͷ�װ��1��B�ͷ�װ����Ҫ����Сʱ��
(2)һ��ʱ���˾�涨����ÿ������ÿ�±���ӹ�A��B�����ͺŵķ�װ���Ҽӹ�A�ͷ�װ����������B�ͷ�װ��һ��������һ����������ÿ�¼ӹ�A�ͷ�װa���������ܶ�ΪWԪ������������ѧ֪ʶ�жϸù�˾��ִ�й涨���Ƿ�Υ���˹���ŵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ҵ���Ŀ�ҵ��Ϊ�����˿ͣ�����һָ���������һ����Ħ�����Σ����˿��г����飬�շ�����ͼ��
��1�����ڴ˰�Ħ����������Ϣ��1Сʱ����Ҫ֧������Ԫ��
��2��ij���ڸ�����һ��������18Ԫ����ô���ڸ������������Ϣ�˶�ã�
��3�������������̳����һ�����ˣ�������˸�֪��ʱ���£�Ԥ��4.5Сʱ����ܵ�������ô���������Ҫ�ڸ�����������Ϣֱ�����˵�������������Ҫ֧������Ǯ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ɱ߳�Ϊ1��С��������ɵ�����ͼ������ABC������ƽ��ֱ������ϵ��O�������ǣ�0��0����
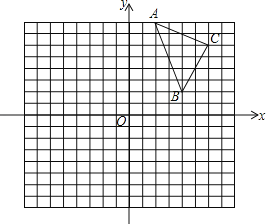
��1����OΪλ�����ģ�����A��B��C���ס�ABC�����Ʊ�Ϊ1��2���ұ�֤��A��B��C���ڵ������ޣ�
��2����B��������� �� ����
��3�����߶�BC����һ��D����������Ϊ��a��b������ô���Ķ�Ӧ��D�������Ϊ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��ı���OABC�Ķ���O������ԭ�㣬��A�ڵ�һ���ޣ���C�ڵ������ޣ���B��x����������ϣ���OAB��90����OA��AB��OB��OC�ij��ֱ��Ƕ�Ԫһ�η�����![]() �Ľ⣨OB��OC����
�Ľ⣨OB��OC����

��1�����A�͵�B�����ꣻ
��2����P���߶�OB�ϵ�һ�����㣨��P�����O��B�غϣ�������P��ֱ��l��y��ƽ�У�ֱ��l����OA���AB�ڵ�Q������OC���BC�ڵ�R�����P�ĺ�����Ϊt���߶�QR�ij���Ϊm����֪t��4ʱ��ֱ��lǡ�ù���C��
�ٵ�0��t��3ʱ����m����t�ĺ�����ϵʽ��
�ڵ�m��![]() ʱ�����P�ĺ�����t��ֵ��
ʱ�����P�ĺ�����t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������7�·ݵ�һ�����ڵ���������ÿ�ɣ��ݣ�25Ԫ�ļ۸����ij�ֽ������Ʋ�Ʒ��2000�ɣ�����ʱ���������ѣ��������Ʋ�Ʒ�ڵڶ������ڵ�����������У�ÿ�ɵ��ǵ�������±�(���������ݱ�ʾ��ǰһ�������ǻ������Ԫ) (��λ��Ԫ)��
���� | һ | �� | �� | �� | �� |
ÿ���ǵ��� |
|
|
|
|
|
��1��д���ڶ�������ÿ��ÿ�����Ʋ�Ʒ�����̼ۣ���ÿ�����ʱ�̵ijɽ��ۣ���
��2����֪���Ʋ�Ʒ����ʱ������������ȡǧ��֮���������ѣ�����������ڵڶ������ڵ������彻����ǰ��ȫ����Ʒ��������������������?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������8�֣���ͼ����֪������y=��x2+bx+c��x�ύ�ڵ�A����1��0���͵�B��3��0������y�ύ�ڵ�C������BC�������ߵĶԳ����ڵ�E��D�������ߵĶ��㣮
��1����������ߵĽ���ʽ��
��2��ֱ��д����C�͵�D�����ꣻ
��3������P�ڵ�һ�����ڵ��������ϣ���S��ABP=4S��COE����P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
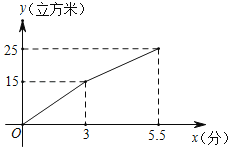
����Ŀ��ij��ˮ�ഢ�������Ϊ25�����ף�����һ������ں�һ������ڣ���ijʱ�̿�ʼ��ֻ������ڣ����������ע��ˮ�࣬3���Ӻ��ٴ�����ڣ����������䳵���ˮ�࣬�־���2.5���Ӵ����ע�����ر�����ڣ�����ԭ��������ٶȼ��������䳵���ˮ�࣬�������ˮ�������ﵽ8������ʱ���ر�����ڣ�������ڵ�ˮ����y�������ף���ʱ��x���֣�֮��IJ��ֺ���ͼ����ͼ��ʾ��
��1����ÿ���������ע���ˮ������
��2����3��x��5.5ʱ����y��x֮��ĺ�����ϵʽ��
��3�������ÿ���������䳵�����ˮ�������� �������ף��Ӵ�����ڵ��ر�����ڹ��õ�ʱ��Ϊ�� �����ӣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com