
 如图,⊙O的半径是3,点P是⊙O上一点,弦AB垂直平分线段OP,点M是弧$\widehat{APB}$上的任意一点(与A、B不重合),MN⊥AB于N,以M为圆心,MN为半径作⊙M,分别过A、B作⊙M的切线,两切线交于点C.
如图,⊙O的半径是3,点P是⊙O上一点,弦AB垂直平分线段OP,点M是弧$\widehat{APB}$上的任意一点(与A、B不重合),MN⊥AB于N,以M为圆心,MN为半径作⊙M,分别过A、B作⊙M的切线,两切线交于点C.分析 (1)连接OA,OP与AB的交点为Q,则△OAQ为直角三角形,且OA=3,OQ=$\frac{3}{2}$,借助勾股定理可求得AQ的长;
(2)判定∠CAB+∠ABC的值是否是定值,由于⊙M是△ABC的内切圆,所以AM和BM分别为∠CAB和∠ABC的角平分线,因此只要∠MAN+∠MBA是定值,那么CAB+∠ABC就是定值,而∠MAN+∠MBA等于弧AB所对的圆周角,这个值等于∠AOB值的一半;
(3)由题可知S=S△ABM+S△ACM+S△BCM=$\frac{1}{2}$(6$\sqrt{3}$+2CE),结合圆M切线的性质推知∠ECM=$\frac{1}{2}$∠ACB=30°,在直角△CEM中,利用勾股定理求得CE的长度,则CD=CE=$\sqrt{3}$ME=$\sqrt{3}$MN.由已知条件S=4$\sqrt{3}$MN2推知4$\sqrt{3}$MN2=$\frac{1}{2}$(6$\sqrt{3}$+2CE)•MN,由此求得MN的值,即圆M的半径.
解答 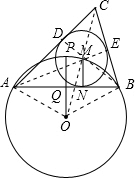 解:(1)连接OA,取OP与AB的交点为Q,则有OA=3.
解:(1)连接OA,取OP与AB的交点为Q,则有OA=3.
∵弦AB垂直平分线段OP,
∴OQ=$\frac{1}{2}$OP=$\frac{3}{2}$,AQ=BQ,
在Rt△OAF中,
∵AQ=$\sqrt{O{A}^{2}-O{Q}^{2}}$=$\sqrt{9-(\frac{3}{2})^{2}}$=$\frac{3\sqrt{3}}{2}$,
∴AB=2AQ=3$\sqrt{3}$.
(2)连接AD、BD,
由(1),OQ=$\frac{3}{2}$,AQ=$\frac{3\sqrt{3}}{2}$,
∴tan∠AOP=$\frac{AQ}{OQ}$=$\sqrt{3}$,
∴∠AOP=60°,
∴∠AOB=120°,
∵点M为△ABC的内心,
∴∠CAB=2∠MAN,∠CBA=2∠MBA,
∵∠MAN+∠MBA=$\frac{1}{2}$∠AOM+$\frac{1}{2}$∠MOB=$\frac{1}{2}$∠AOB=60°,
∴∠CAB+∠CBA=120°,
∴∠ACB=60°.
(3)取AC、BC与圆M的切点分别是D、E,连接OM、MD、MC、ME,则有MD=ME=MN,MD⊥AC,ME⊥MC,
∴S=S△ABM+S△ACM+S△BCM=$\frac{1}{2}$AB•MN+$\frac{1}{2}$BC•ME+$\frac{1}{2}$AC•MD=$\frac{1}{2}$(AB+BC+AC)•MN=$\frac{1}{2}$(6$\sqrt{3}$+2CE),
∵DE、CD是圆M的切线,
∴∠ECM=$\frac{1}{2}$∠ACB=30°,
∴在直角△CEM中,CE=$\sqrt{3}$ME,
∴CD=CE=$\sqrt{3}$ME=$\sqrt{3}$MN.
∵S=4$\sqrt{3}$MN2,
∴4$\sqrt{3}$MN2=$\frac{1}{2}$(6$\sqrt{3}$+2CE)•MN,
∴MN=1,即圆M的半径是1.
点评 本题巧妙将垂径定理、勾股定理、内切圆、切线长定理、三角形面积等知识综合在一起,需要考生从前往后按顺序解题,前面问题为后面问题的解决提供思路,是一道难度较大的综合题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
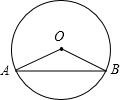 (1)如图,弦AB把⊙O分成2:7,∠AOB=80°;
(1)如图,弦AB把⊙O分成2:7,∠AOB=80°;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在长方形ABCD中,AD=8cm,CD=4cm.
如图,在长方形ABCD中,AD=8cm,CD=4cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com