
【题目】A、B两地相距90km,甲、乙两人从两地出发相向而行,甲先出发.图中l1,l2表示两人离A地的距离S(km)与时间t(h)的关系,结合图象回答下列问题
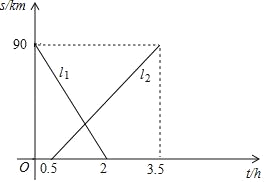
(1)表示甲离A地的距离与时间关系的图象是 (填l1或l2);
(2)甲的速度是 km/h;乙的速度是 km/h
(3)甲出发后多少时间两人相遇?
【答案】(1)l1;;(2)45,30;;(3)1.4小时
【解析】
(1)根据甲先出发和图像的关系即可得出;
(2)有图可知甲2小时行驶了90km,故甲的速度为90÷2=45km/h,乙(3.5-0.5)小时行驶了90km乙的速度是:90÷(3.5﹣0.5)=90÷3=30km/h;
(3)利用待定系数法求出l1和l2的函数解析式,求出其交点坐标横即可.
解:(1)∵甲先出发,
∴表示甲离A地的距离与时间关系的图象是l1,
故答案为:l1;
(2)甲的速度是:90÷2=45km/h,乙的速度是:90÷(3.5﹣0.5)=90÷3=30km/h,
故答案为:45,30;
(3)设甲对应的函数解析式为y=ax+b,
![]() ,解得
,解得![]() ,
,
∴甲对应的函数解析式为y=﹣45x+90,
设乙对应的函数解析式为y=cx+d,
![]() ,解得
,解得![]() ,
,
即乙对应的函数解析式为y=30x﹣15,
![]() ,解得
,解得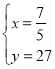 .
.
答:甲出发1.4小时后两人相遇.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6cm,BC=12cm.. 点M从点A开始沿AB边向点B以1cm/秒的速度向B点移动,点N从点B开始沿BC边以2cm/秒的速度向点C移动. 若M, N分别从A, B点同时出发,设移动时间为t (0<t<6),△DMN的面积为S.
(1) 求S关于t的函数关系式,并求出S的最小值;
(2) 当△DMN为直角三角形时,求△DMN的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某开发商的经适房的三个居民小区A、B、C在同一条直线上,位置如图所示.其中小区B到小区A、C的距离分别是70m和150m,现在想在小区A、C之间建立一个超市,要求各小区居民到超市总路程的和最小,那么超市的位置应建在( )
![]()
A.小区AB.小区BC.小区CD.AC的中点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学课上,张老师出示了一个题目:“如图,ABCD的对角线相交于点O,过点O作EF垂直于BD交AB,CD分别于点F,E,连接DF,BE.请根据上述条件,写出一个正确结论.”其中四位同学写出的结论如下:
小青:OE=OF;小何:四边形DFBE是正方形;
小夏:S四边形AFED=S四边形FBCE;小雨:∠ACE=∠CAF.
这四位同学写出的结论中不正确的是( )

A. 小青 B. 小何 C. 小夏 D. 小雨
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年6月6日,工信部正式向四家电信企业发放![]() 商用牌照,标志着
商用牌照,标志着![]() 元年开始华为公司作为
元年开始华为公司作为![]() 行业的领军者,已经具备从芯片、产品到系统组网的世界领先的
行业的领军者,已经具备从芯片、产品到系统组网的世界领先的![]() 技术,是全球唯一一家能够提供端到端
技术,是全球唯一一家能够提供端到端![]() 商用解决方案的通讯企业为了了解某中学生对
商用解决方案的通讯企业为了了解某中学生对![]() 通讯技术的了解情况,随机抽取部分学生进行问卷,将结果分成“非常了解”“比较了解”、“一般了解”、“不了解”四种类型,分别记为
通讯技术的了解情况,随机抽取部分学生进行问卷,将结果分成“非常了解”“比较了解”、“一般了解”、“不了解”四种类型,分别记为![]() ,根据调查结果给制了如下尚不完整的两个统计图
,根据调查结果给制了如下尚不完整的两个统计图
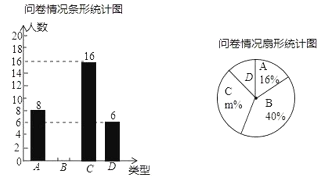
(1)本次问卷共随机调查了 名学生,在扇形统计图中![]() _ _,“
_ _,“![]() ”所在扇形的圆心角的度数为 度;
”所在扇形的圆心角的度数为 度;
(2)请根据数据信息补全条形统计图;
(3)若该校有![]() 名学生,估计选择“非常了解”、“比较了解”的学生共约有多少人?
名学生,估计选择“非常了解”、“比较了解”的学生共约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(0,2),B(4,0),C(4,3)三点.
(1)建立平面直角坐标系并描出A、B、C三点
(2)求△ABC的面积;
(3)如果在第二象限内有一点P(m,1),且四边形ABOP的面积是△ABC的面积的两倍;求满足条件的P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某机动车出发前油箱内有油![]() .行驶若干小时后,途中在加油站加油若干升.油箱中剩余油量
.行驶若干小时后,途中在加油站加油若干升.油箱中剩余油量![]() 与行驶时间
与行驶时间![]() 之间的关系如图所示,根据图像回答问题.
之间的关系如图所示,根据图像回答问题.

(1)机动车行驶几小时后加油?
(2)中途加油_____________![]() ;
;
(3)如果加油站距目的地还有![]() ,车速为
,车速为![]() ,要到达目的地,油箱中的油是否够用?并说明原因.
,要到达目的地,油箱中的油是否够用?并说明原因.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com